 por JailsonJr » Sex Mai 14, 2010 07:10
por JailsonJr » Sex Mai 14, 2010 07:10
Se
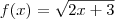
, então
![[f( \sqrt{2} ) - f( - \sqrt{2} )]^2 [f( \sqrt{2} ) - f( - \sqrt{2} )]^2](/latexrender/pictures/3b7b4ee97063d26ccd56f49ffb0cd6cc.png)
é igual a:
Resp.: 4

-
JailsonJr
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Sex Mai 14, 2010 06:51
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por vyhonda » Sex Mai 14, 2010 11:12
por vyhonda » Sex Mai 14, 2010 11:12
Sabendo que
![f(x)=\sqrt[]{2x + 3} f(x)=\sqrt[]{2x + 3}](/latexrender/pictures/4b06dbbec3dc62d227d66f5817f82026.png)
, basta substituir
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
em x, assim:
![f(\sqrt[]{2}) = \sqrt[]{2\sqrt[]{ 2} + 3} f(\sqrt[]{2}) = \sqrt[]{2\sqrt[]{ 2} + 3}](/latexrender/pictures/98875f525852709c5152422c6c69462a.png)
=> I
![f(-\sqrt[]{2}) = \sqrt[]{(2 . - \sqrt[]{ 2}) + 3} f(-\sqrt[]{2}) = \sqrt[]{(2 . - \sqrt[]{ 2}) + 3}](/latexrender/pictures/268e268323d31538f0fcd1b2d1387612.png)
=> II
Substituindo Equação I e II na expressão
![{ [ f(\sqrt[]{2}) - f(-\sqrt[]{2}) ] }^{2} { [ f(\sqrt[]{2}) - f(-\sqrt[]{2}) ] }^{2}](/latexrender/pictures/9f6cf647574630bdd60012f5c4ea4106.png)
![{[ \sqrt[]{2\sqrt[]{2}+3} - \sqrt[]{(2. - \sqrt[]{2})+3} ]}^{2} {[ \sqrt[]{2\sqrt[]{2}+3} - \sqrt[]{(2. - \sqrt[]{2})+3} ]}^{2}](/latexrender/pictures/c316136aea6bb7f100a34dd19fb773ec.png)
, temos o Quadrado da Diferença
Aplicando fatoração::
![2\sqrt[]{2}+3 -2[\sqrt[]{2\sqrt[]{2}+3}.\sqrt[]{-2\sqrt[]{2}+3}] + (-2\sqrt[]{2} + 3) 2\sqrt[]{2}+3 -2[\sqrt[]{2\sqrt[]{2}+3}.\sqrt[]{-2\sqrt[]{2}+3}] + (-2\sqrt[]{2} + 3)](/latexrender/pictures/8d7e71115079421cad051af69d9159db.png)
![2\sqrt[]{2} -2\sqrt[]{2} +3+ 3 -2[\sqrt[]{2\sqrt[]{2}+3}.\sqrt[]{-2\sqrt[]{2}+3}] 2\sqrt[]{2} -2\sqrt[]{2} +3+ 3 -2[\sqrt[]{2\sqrt[]{2}+3}.\sqrt[]{-2\sqrt[]{2}+3}]](/latexrender/pictures/4fae476740e56f9baef9ff648d28febd.png)
![6 -2[-4.2 + 6\sqrt[]{2} - 6\sqrt[]{2} + 9] 6 -2[-4.2 + 6\sqrt[]{2} - 6\sqrt[]{2} + 9]](/latexrender/pictures/73b280b6a89e9fe5829bdd0ddb2210db.png)
![6 -2[-8 + 9] 6 -2[-8 + 9]](/latexrender/pictures/587a97772929b60d518112d0392daa13.png)
6 - 2[1]
Portanto Resposta = 4.
Quaquer dúvida na conta, é só perguntar
Bons estudos!
-
vyhonda
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Dom Jan 17, 2010 20:03
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Materiais - Unesp
- Andamento: cursando
 por JailsonJr » Sex Mai 14, 2010 12:00
por JailsonJr » Sex Mai 14, 2010 12:00
Obrigado, entendi perfeitamente!

-
JailsonJr
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Sex Mai 14, 2010 06:51
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função real definida pela soma de uma função par c/uma ímpar
por Taah » Sáb Mar 27, 2010 15:33
- 3 Respostas
- 5588 Exibições
- Última mensagem por Taah

Dom Mar 28, 2010 13:21
Funções
-
- [plano tangente a função de duas variaveis dada por função]
por isaac naruto » Qui Dez 31, 2015 16:35
- 0 Respostas
- 4592 Exibições
- Última mensagem por isaac naruto

Qui Dez 31, 2015 16:35
Cálculo: Limites, Derivadas e Integrais
-
- [Desigualdade] entre função exponencial e função potência
por VitorFN » Sex Mai 26, 2017 15:18
- 1 Respostas
- 5751 Exibições
- Última mensagem por adauto martins

Sex Jul 07, 2017 12:17
Álgebra Elementar
-
- +uma função das trevas.ajuda aew!(função par mas heim!?)
por Fabricio dalla » Dom Fev 27, 2011 16:12
- 2 Respostas
- 3490 Exibições
- Última mensagem por LuizAquino

Dom Mar 06, 2011 09:17
Funções
-
- [FUNÇÃO] Não consigo achar a fórmula da função
por LAZAROTTI » Qui Set 27, 2012 00:06
- 1 Respostas
- 2959 Exibições
- Última mensagem por MarceloFantini

Qui Set 27, 2012 07:13
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
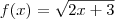 , então
, então ![[f( \sqrt{2} ) - f( - \sqrt{2} )]^2 [f( \sqrt{2} ) - f( - \sqrt{2} )]^2](/latexrender/pictures/3b7b4ee97063d26ccd56f49ffb0cd6cc.png) é igual a:
é igual a:
![f(x)=\sqrt[]{2x + 3} f(x)=\sqrt[]{2x + 3}](/latexrender/pictures/4b06dbbec3dc62d227d66f5817f82026.png) , basta substituir
, basta substituir ![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) em x, assim:
em x, assim:![f(\sqrt[]{2}) = \sqrt[]{2\sqrt[]{ 2} + 3} f(\sqrt[]{2}) = \sqrt[]{2\sqrt[]{ 2} + 3}](/latexrender/pictures/98875f525852709c5152422c6c69462a.png) => I
=> I![f(-\sqrt[]{2}) = \sqrt[]{(2 . - \sqrt[]{ 2}) + 3} f(-\sqrt[]{2}) = \sqrt[]{(2 . - \sqrt[]{ 2}) + 3}](/latexrender/pictures/268e268323d31538f0fcd1b2d1387612.png) => II
=> II![{ [ f(\sqrt[]{2}) - f(-\sqrt[]{2}) ] }^{2} { [ f(\sqrt[]{2}) - f(-\sqrt[]{2}) ] }^{2}](/latexrender/pictures/9f6cf647574630bdd60012f5c4ea4106.png)
![{[ \sqrt[]{2\sqrt[]{2}+3} - \sqrt[]{(2. - \sqrt[]{2})+3} ]}^{2} {[ \sqrt[]{2\sqrt[]{2}+3} - \sqrt[]{(2. - \sqrt[]{2})+3} ]}^{2}](/latexrender/pictures/c316136aea6bb7f100a34dd19fb773ec.png) , temos o Quadrado da Diferença
, temos o Quadrado da Diferença![2\sqrt[]{2}+3 -2[\sqrt[]{2\sqrt[]{2}+3}.\sqrt[]{-2\sqrt[]{2}+3}] + (-2\sqrt[]{2} + 3) 2\sqrt[]{2}+3 -2[\sqrt[]{2\sqrt[]{2}+3}.\sqrt[]{-2\sqrt[]{2}+3}] + (-2\sqrt[]{2} + 3)](/latexrender/pictures/8d7e71115079421cad051af69d9159db.png)
![2\sqrt[]{2} -2\sqrt[]{2} +3+ 3 -2[\sqrt[]{2\sqrt[]{2}+3}.\sqrt[]{-2\sqrt[]{2}+3}] 2\sqrt[]{2} -2\sqrt[]{2} +3+ 3 -2[\sqrt[]{2\sqrt[]{2}+3}.\sqrt[]{-2\sqrt[]{2}+3}]](/latexrender/pictures/4fae476740e56f9baef9ff648d28febd.png)
![6 -2[-4.2 + 6\sqrt[]{2} - 6\sqrt[]{2} + 9] 6 -2[-4.2 + 6\sqrt[]{2} - 6\sqrt[]{2} + 9]](/latexrender/pictures/73b280b6a89e9fe5829bdd0ddb2210db.png)
![6 -2[-8 + 9] 6 -2[-8 + 9]](/latexrender/pictures/587a97772929b60d518112d0392daa13.png)



 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.