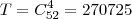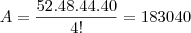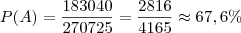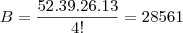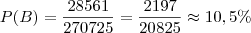Probabilidade

[Douglaspimentel]

Um baralho comum consiste de 52 cartasseparadas em 4 naipes com 13 cartas de cada um.
Para cada naipe , os valores são 2,3,4,5,6,7,8,9,10,J,Q,K e A. Um baralho comum é embaralhado.
Qual a probabilidade de que as 4 cartas do topo tenham:

a) Valores diferentes?
b) Naipes diferenres?

[luucas]

alguém pode me ajudar em estatistica estou com muita dificuldade em resposder este exercicio.

Através de pesquisas, identificou-se que os candidatos a vendedor, despendem, em média, em um dos testes para contratação, 50 minutos em média com desvio padrão de 15 minutos. A distribuição do tempo de resposta é aproximadamente normal.

a) Que porcentagem de candidatos levará menos de 50 minutos para concluir o teste?

b) Que porcentagem não terminará o teste se o tempo máximo concedido é de 90 minutos?

c) Se 50 candidatos fazem o teste, quantos podem esperar que o terminem nos primeiros 40 minutos?


obrigado!

[Douglasm]

Primeiramente: Lucas, caso queira ajuda para solucionar um problema, abra um novo tópico.

Agora respondendo a pergunta do Douglas:

Comecemos determinando o número de casos possíveis (T):



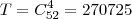
Esse número é o total de combinações de 4 cartas, haja vista que a ordem em que elas aparecem não é relevante.

Agora passemos a letra A:

Nessa situação, os casos favoráveis serão aqueles em que cartas de mesmo valor não aparecem na combinação. Então temos:



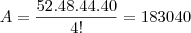
Obs: Acima foi feito o seguinte raciocínio: Inicialmente a primeira carta pode ser qualquer uma (52); a segunda pode ser qualquer uma menos as quatro com o mesmo valor da primeira; a terceira pode ser qualquer uma menos as oito cartas correspondentes aos valores da primeira e da segunda; a quarta pode ser qualquer uma menos as 12 cartas correspondentes aos valores anteriores (lembrando que cada carta tem 4 naipes). Levando em conta que a ordem que elas aparecem é irrelevante, devemos dividir esse produto por 4! (que são as permutações das cartas entre si).

A probabilidade é, portanto:



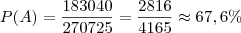
Letra B:



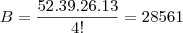
(Foi feito um raciocício análogo ao anterior)



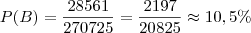
Seria interessante se você tivesse a resposta para conferirmos. Até a próxima.