Olá, Fábio, tudo bem?
Estava estudando quando me deparei com a seguinte questão:
A razão entre as idades de um pai e seu filho é de 5/2. Se o pai tinha 21 anos quando seu filho nasceu, qual a idade do filho?
Tentei resolver assim, porém não sei se estou certo:
Chamei o pai de x; e o filho de y. Então montei um sistema:
x/y=5/2 I
x=21+y II
Resolvendo: substituindo II em I, obtive:
21+y/y=5/2 --> 2(21+y)=5y --> -3y= -42 (-1)
y= 14 anos
x= 35 anos
Então a idade do filho seria 14 anos. Está certo o meu raciocínio?
Desde já agradeço a sua ajuda que é de grande importância para os meus estudos. Tenha uma boa noite!



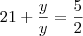

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)