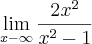
No meu gabarito a resposta é 2, mas eu não consigo chegar nesse número.
Grato
Mario

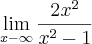





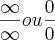


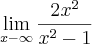
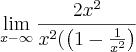

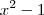 , e colocou
, e colocou  em evidência. Veja só:
em evidência. Veja só: 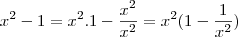
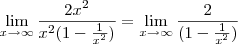
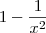 tende a ser 1. (note que
tende a ser 1. (note que 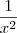 é um número infinitamente pequeno nesse caso, portanto tende a zero.)
é um número infinitamente pequeno nesse caso, portanto tende a zero.)
 Eu não consegui entender essa colocação do
Eu não consegui entender essa colocação do  em evidência
em evidência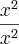 e depois ele vira
e depois ele vira 
 vira 1 e o denominador continua
vira 1 e o denominador continua  se o
se o  está multiplicando também.
está multiplicando também. do numerador vira 1 porque o
do numerador vira 1 porque o  do denomimador também não vira 1
do denomimador também não vira 1
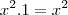 e que
e que 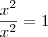 ?
?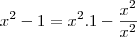
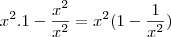
 multiplicado por
multiplicado por  menos
menos  multiplicado por
multiplicado por  é igual ao nosso denominador
é igual ao nosso denominador 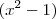 .
.
 , se x
, se x 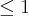


Douglasm escreveu:O melhor é abrir outro tópico para uma nova questão, mas me diga, o que você que saber a respeito dessa função?








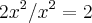


Douglasm escreveu:Para falar a verdade, eu não sei um jeito melhor de explicar isso que o dele. (Que aliás está bem elucidativo.) Se você pensar que para um função ser derivável, ela deve apresentar derivadas laterais idênticas quando x tende a um determinado valor, no seu caso o 1, verá que essa sua função que forma um "bico" não é derivável nesse ponto. Me desculpe, mas realmente não sei explicar de um jeito mais simples.
Até a próxima.

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)