(onde tem-se o simbolo de "+", lê-se: ''pela direita'')
Obrigada
Abraços!
por EulaCarrara » Seg Abr 19, 2010 21:29
por MarceloFantini » Seg Abr 19, 2010 22:01
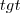. Quando t se aproxima de 
pela direita, os valores vão decrescendo vertiginosamente, tornando a tangente um número extremamente pequeno e negativo. Isso é importante, pois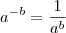 
, fazendo com que o limite seja 
, onde 
é elevado a um número muito grande, e dessa maneira o denominador cresce de maneira descontrolada, obrigando a fração a se tornar um valor cada vez mais próximo de zero. Assim:
por EulaCarrara » Seg Abr 19, 2010 22:07
por EulaCarrara » Seg Abr 19, 2010 22:13
por MarceloFantini » Seg Abr 19, 2010 23:11
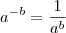, que no caso do exercício, era .Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a 
e elevar ao quadrado os dois lados)