Pergunta - se:
a) Quantos fazem capoeira e nao fazem musculaçao? R: 54 alunos
b) Quantos fazem natacao e capoeira e nao fazem musculaçao? R: 90 alunos
Bom me confundi toda com essas porcentagens, e nao cheguei nem perto da reposta correta!!
Tenho este outro do ITA, que simplesmente nem sei por onde começa, se puderem me dar uma dica!
Sejam U um conjunto nao vazio e A
 U, B
U, B U.
U.Usando apenas as definicoes de igualdade, uniao, intersecçao e complementar, prove que:
I. Se A
 B= conj. vazio, entao B
B= conj. vazio, entao B
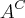
II. B\
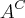 =B
=B A
ANotaçoes: A\B = {x
 A; x nao pertence B}
A; x nao pertence B}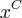 = U\X, para x
= U\X, para x U, U
U, U conj. vazio
conj. vazio



 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.