(UFSCar-SP-2009) A parábola determinada pela função f: R->R tal que f(x) = ax^2+bx+c, com a != 0 (diferente de 0), tem vértice nas coordenadas (4,2). Se o ponto de coordenadas (2,0) pertence ao gráfico desta função, então o produto abc é igual a:
Eu não sei a resposta pq foi de um simulado que eu fiz, e essa questão foi a única que não consegui fazer! Poderiam me ajudar?
Abras





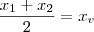
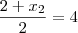
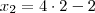
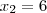

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)