


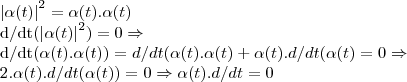




guilherme5088 escreveu:Seja α(t) uma curva parametrizada que não passa pela origem. Se α(to) é o ponto do traço de α mais próximo da origem e α'(to) é diferente de 0. Mostre que o vetor posição α(t) é ortogonal a α'(to).

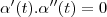

LuizAquino escreveu:guilherme5088 escreveu:Seja α(t) uma curva parametrizada que não passa pela origem. Se α(to) é o ponto do traço de α mais próximo da origem e α'(to) é diferente de 0. Mostre que o vetor posição α(t) é ortogonal a α'(to).
Olá Guilherme, veja minha resolução neste vídeo:
https://www.youtube.com/watch?v=1XRFbaIvguQ
Eu espero que isso possa ajudar!

guilherme5088 escreveu:Sou inscrito no seu canal, professor. Muito bom o vídeo.


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)