 por adauto martins » Qui Out 15, 2020 16:14
por adauto martins » Qui Out 15, 2020 16:14
mostre que entre dois numeros racionais,existem infinitos numeros irracionais.
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Qui Out 15, 2020 16:31
por adauto martins » Qui Out 15, 2020 16:31
de fato,pois
tomemos o numero
![\sqrt[k]{{p}_{j}},{p}_{j}numero primo...p/k,j\in N \sqrt[k]{{p}_{j}},{p}_{j}numero primo...p/k,j\in N](/latexrender/pictures/8abe8ec163d7d722c4eee7f9d64a5a49.png)
que é um numero irracional
temos que
![{p}_{j}-1\prec \sqrt[k]{{p}_{j}}\prec {p}_{j}\Rightarrow {p}_{j}-1\prec \sqrt[k]{{p}_{j}}\prec {p}_{j}\Rightarrow](/latexrender/pictures/60ffca3a148aaae0dbccdc08954da867.png)
![(p-1)/q\prec({p}_{j}-1)/q\prec \sqrt[k]{{p}_{j}}/q\prec {p}_{j}/q \prec p/q (p-1)/q\prec({p}_{j}-1)/q\prec \sqrt[k]{{p}_{j}}/q\prec {p}_{j}/q \prec p/q](/latexrender/pictures/bf77ba90d318ed98c6ea19d65da70fe3.png)
...
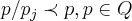
e
p,q primos entre si...
analogo p/ entre dois irracionais,existem infinitos racionais(fica como exercicio)
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Qui Out 15, 2020 18:38
por adauto martins » Qui Out 15, 2020 18:38
a soluçao acima apresenta esta incorreta,vamos a soluçao correta.
tomemos,como visto acima
![r\prec \sqrt[k]{{p}_{j}}\prec p r\prec \sqrt[k]{{p}_{j}}\prec p](/latexrender/pictures/36292cdbdb71b218d48d352a3d4fe34a.png)
para p,r racionais...logo,podemos ter:
![\sqrt[k]{{p}_{j}}-1\prec \sqrt[k]{{p}_{j}}\prec{p}_{j} \sqrt[k]{{p}_{j}}-1\prec \sqrt[k]{{p}_{j}}\prec{p}_{j}](/latexrender/pictures/c39c29133141f971e89a136ef938e541.png)
...
![(r-1)/q\prec(\sqrt[k]{{p}_{j}}-1)/q\prec \sqrt[k]{{p}_{j}}/q\prec {p}_{j}/q\prec p/q (r-1)/q\prec(\sqrt[k]{{p}_{j}}-1)/q\prec \sqrt[k]{{p}_{j}}/q\prec {p}_{j}/q\prec p/q](/latexrender/pictures/cda318157c5712f28e6c6062ad61f2d7.png)
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Teoria dos Números
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- exercicio resolvido
por adauto martins » Sex Jul 15, 2016 14:48
- 0 Respostas
- 33703 Exibições
- Última mensagem por adauto martins

Sex Jul 15, 2016 14:48
Teoria dos Números
-
- exercicio resolvido
por adauto martins » Qua Jul 20, 2016 18:35
- 0 Respostas
- 31787 Exibições
- Última mensagem por adauto martins

Qua Jul 20, 2016 18:35
Cálculo: Limites, Derivadas e Integrais
-
- exercicio resolvido
por adauto martins » Ter Jul 26, 2016 17:43
- 0 Respostas
- 22017 Exibições
- Última mensagem por adauto martins

Ter Jul 26, 2016 17:43
Cálculo: Limites, Derivadas e Integrais
-
- exercicio resolvido
por adauto martins » Sáb Ago 13, 2016 11:28
- 0 Respostas
- 17069 Exibições
- Última mensagem por adauto martins

Sáb Ago 13, 2016 11:28
Teoria dos Números
-
- exercicio resolvido
por adauto martins » Sex Out 18, 2019 14:29
- 2 Respostas
- 22856 Exibições
- Última mensagem por adauto martins

Sex Out 18, 2019 15:42
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



![\sqrt[k]{{p}_{j}},{p}_{j}numero primo...p/k,j\in N \sqrt[k]{{p}_{j}},{p}_{j}numero primo...p/k,j\in N](/latexrender/pictures/8abe8ec163d7d722c4eee7f9d64a5a49.png) que é um numero irracional
que é um numero irracional![{p}_{j}-1\prec \sqrt[k]{{p}_{j}}\prec {p}_{j}\Rightarrow {p}_{j}-1\prec \sqrt[k]{{p}_{j}}\prec {p}_{j}\Rightarrow](/latexrender/pictures/60ffca3a148aaae0dbccdc08954da867.png)
![(p-1)/q\prec({p}_{j}-1)/q\prec \sqrt[k]{{p}_{j}}/q\prec {p}_{j}/q \prec p/q (p-1)/q\prec({p}_{j}-1)/q\prec \sqrt[k]{{p}_{j}}/q\prec {p}_{j}/q \prec p/q](/latexrender/pictures/bf77ba90d318ed98c6ea19d65da70fe3.png) ...
...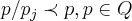

![r\prec \sqrt[k]{{p}_{j}}\prec p r\prec \sqrt[k]{{p}_{j}}\prec p](/latexrender/pictures/36292cdbdb71b218d48d352a3d4fe34a.png)
![\sqrt[k]{{p}_{j}}-1\prec \sqrt[k]{{p}_{j}}\prec{p}_{j} \sqrt[k]{{p}_{j}}-1\prec \sqrt[k]{{p}_{j}}\prec{p}_{j}](/latexrender/pictures/c39c29133141f971e89a136ef938e541.png) ...
...![(r-1)/q\prec(\sqrt[k]{{p}_{j}}-1)/q\prec \sqrt[k]{{p}_{j}}/q\prec {p}_{j}/q\prec p/q (r-1)/q\prec(\sqrt[k]{{p}_{j}}-1)/q\prec \sqrt[k]{{p}_{j}}/q\prec {p}_{j}/q\prec p/q](/latexrender/pictures/cda318157c5712f28e6c6062ad61f2d7.png)

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
