Pessoal, bom dia!
Um exercício que ao ver parece bem fácil, mas não consigo chegar a um cálculo correto de jeito nenhum. Penso que ele é passivo de uma análise combinatória, só que não sei como resolver. Na verdade, não sei nem como começar. Alguém poderia me dar um help?
O exercício é o seguinte:
Em um shopping existe uma máquina de surpresas (de quantidade infinita, pois o seu conteúdo nunca acabará), onde a cada tentativa, tenho 60% de obter uma surpresa normal, 37,5% de obter uma surpresa rara, e 2,5% de chance de obter uma surpresa especial. Com o objetivo de aumentar as minhas chances de obter uma surpresa especial, [b]adquiri 28 tentativas.
Qual será a minha probabilidade de obter pelo menos 1 surpresa especial?[/b]
Me ajudarão MUUUITO
Obrigado pela atenção


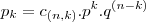
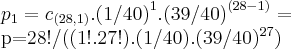 ...
...
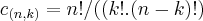
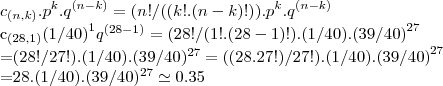
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)