(ITA-exame 1953 )
calcular o volume do solido gerado por um triangulo retangulo isosceles,cujos catetos medem 3m,ao girar em torno da paralela
a hipotenusa traçada pelo vertice do angulo reto.



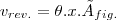
 ´ angulo de rotaçao ´
´ angulo de rotaçao ´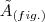 ´ que em nosso casso,sera
´ que em nosso casso,sera
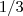 da base e
da base e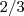 do vertice.em nosso caso o triangulo girara em tórno da paralela a hipotenusa,passando pela origem A do sistema,entao
do vertice.em nosso caso o triangulo girara em tórno da paralela a hipotenusa,passando pela origem A do sistema,entao 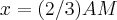
![´h=\sqrt[]{({3}^{2}+{3}^{2})}=3\sqrt[]{2} ´h=\sqrt[]{({3}^{2}+{3}^{2})}=3\sqrt[]{2}](/latexrender/pictures/7568829354a4b6d64239ea6245f2f79e.png) ´
´![AM=BD=DC=(1/2)h=(1/2)3.\sqrt[]{2} AM=BD=DC=(1/2)h=(1/2)3.\sqrt[]{2}](/latexrender/pictures/3624c03322b74e4612f56dcd37a720c6.png) ´
´![x=(2/3)AM=(2/3).(1/2)3.\sqrt[]{2}=\sqrt[]{2} x=(2/3)AM=(2/3).(1/2)3.\sqrt[]{2}=\sqrt[]{2}](/latexrender/pictures/d2303e90bd5282b58dfaa73610b6436b.png) ´
´![{v}_{rev.}=\theta.x.A=2.\pi.\sqrt[]{2}.(9/2)=9\pi\sqrt[]{2} {v}_{rev.}=\theta.x.A=2.\pi.\sqrt[]{2}.(9/2)=9\pi\sqrt[]{2}](/latexrender/pictures/e56aec43df9f5214e2de6ee07c134f9e.png)

Voltar para Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)