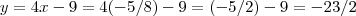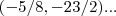por adauto martins » Sex Out 25, 2019 23:19
por adauto martins » Sex Out 25, 2019 23:19
(Este-escola tecnica do exercito-exame de admissao 1952)
achar os pontos de intersecçao das tangentes a curva

nos pontos P(2,4) e Q(-3,9).
PS-a Este passou a ser o IME(instituto militar de engenharia) apartir de 1958.
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Sex Out 25, 2019 23:32
por adauto martins » Sex Out 25, 2019 23:32
soluçao:
aqui vamos calcular a equaçao das retas tangentes aos devidos pontos,e buscar a intersecçao dessas duas retas,que é o pedido do problema.
seja
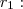
a reta tang. que passa por P(3,9)...
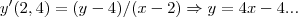
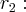
que passa pelo ponto (-3,9)
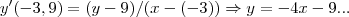
a
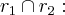
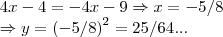
logo:
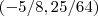
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Sáb Out 26, 2019 10:30
por adauto martins » Sáb Out 26, 2019 10:30
uma correçao:
calculei errado a ordenada y,do ponto de intersecçao,cujo valor
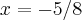
substitui em qquer dos ys,da intersecçao,a saber
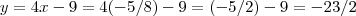
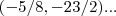
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 nos pontos P(2,4) e Q(-3,9).
nos pontos P(2,4) e Q(-3,9).
 nos pontos P(2,4) e Q(-3,9).
nos pontos P(2,4) e Q(-3,9).
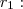 a reta tang. que passa por P(3,9)...
a reta tang. que passa por P(3,9)...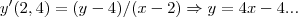
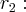 que passa pelo ponto (-3,9)
que passa pelo ponto (-3,9)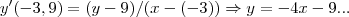
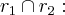
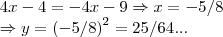
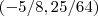

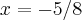 substitui em qquer dos ys,da intersecçao,a saber
substitui em qquer dos ys,da intersecçao,a saber