 por adauto martins » Sex Out 25, 2019 15:18
por adauto martins » Sex Out 25, 2019 15:18
(Este-escola tecnica do exercito-exame de admissao 1937)
derivar a expressao
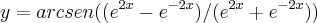
ps-a Este(escola tecnica do exercito) veio a se tornar o atual IME.e deu origem ao primeiro curso de engenharia aeronautica(1939),que depois veio a se tornar o ITA(instituto tecnologico de aeronautica) em 1950.
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Sex Out 25, 2019 15:57
por adauto martins » Sex Out 25, 2019 15:57
soluçao:
podemos derivar y,de duas maneira,que na verdade é a mesma tecnica,ou seja.
podemos usar
![y'=u'/(\sqrt[]{1-{u}^{2}}) y'=u'/(\sqrt[]{1-{u}^{2}})](/latexrender/pictures/017ce60f529aec203a9d2194bc1918f2.png)
,para
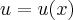
,
ou usar a derivada da funçao implicita,que é a que usaremos:
seja
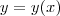
tal que:
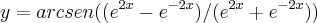
logo,podemos:
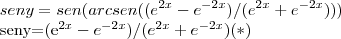
derivando em relaçao a x,teremos:
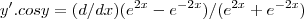
vamos usar aqui a derivada do quociente
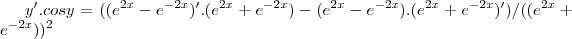
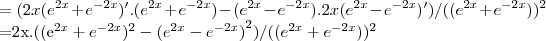
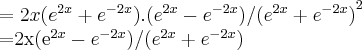
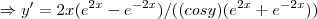
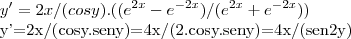
usando a equaçao (*),teremos:
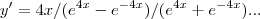
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
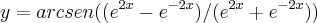

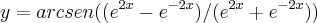

![y'=u'/(\sqrt[]{1-{u}^{2}}) y'=u'/(\sqrt[]{1-{u}^{2}})](/latexrender/pictures/017ce60f529aec203a9d2194bc1918f2.png) ,para
,para 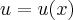 ,
,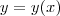 tal que:
tal que: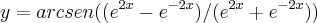
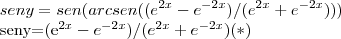
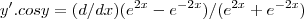
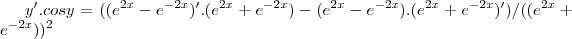
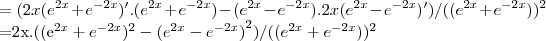
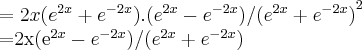
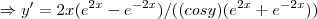
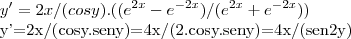
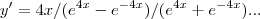

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.