(escola nacional de quimica da universidade do brasil,rj-exame de admissao 1946)
um ponto luminoso esta a 2 m de uma esfera luminosa de raio igual a 4 m.qual e o valor da area da porçao iluminada da esfera?



 ,onde r,raio da esfera(r=4m) e x,a distancia do plano de corte da calota ao ponto exterior da esfera.com os dados que temos,teremos q. determinar x,e faremos isso usando semelhança de triangulos,que sao retangulos...haja imaginaçao...vamos la.o triangulo
,onde r,raio da esfera(r=4m) e x,a distancia do plano de corte da calota ao ponto exterior da esfera.com os dados que temos,teremos q. determinar x,e faremos isso usando semelhança de triangulos,que sao retangulos...haja imaginaçao...vamos la.o triangulo 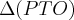 e reto em T,pois toda reta q. tangencia uma esfera,ou uma circunferencia dessa esfera,faz angulo reto com seu raio.dentro desse triangulo(PTO)construamos outro triangulo,q. e tambem retangulo...tomaremos o plano de corte,um ponto q. esta na reta q. une os pontos PO,e chamaremos de k...o triang.(PkT) e retangulo...tomaremos as devidas proporçoes de lado,pois o triang.PTO e semelhante ao triang.PkT,o que e facil de prova...
e reto em T,pois toda reta q. tangencia uma esfera,ou uma circunferencia dessa esfera,faz angulo reto com seu raio.dentro desse triangulo(PTO)construamos outro triangulo,q. e tambem retangulo...tomaremos o plano de corte,um ponto q. esta na reta q. une os pontos PO,e chamaremos de k...o triang.(PkT) e retangulo...tomaremos as devidas proporçoes de lado,pois o triang.PTO e semelhante ao triang.PkT,o que e facil de prova...![PT=\sqrt[]{{(r+2)}^{2}-{r}^{2}}=\sqrt[]{({4+2})^{2}-{4}^{2}}
=\sqrt[]{20}=2.\sqrt[]{5}... PT=\sqrt[]{{(r+2)}^{2}-{r}^{2}}=\sqrt[]{({4+2})^{2}-{4}^{2}}
=\sqrt[]{20}=2.\sqrt[]{5}...](/latexrender/pictures/37ce78b648c5d086d1aab2019c1ca269.png) ...entao:
...entao:![kP/PT=PT/PO\Rightarrow x+2/(2.\sqrt[]{5})=2.\sqrt[]{5}/6
x+2={(2.\sqrt[]{5}})^{2}/6=20/6=10/3 kP/PT=PT/PO\Rightarrow x+2/(2.\sqrt[]{5})=2.\sqrt[]{5}/6
x+2={(2.\sqrt[]{5}})^{2}/6=20/6=10/3](/latexrender/pictures/3547555f6ab799ff0e479fd79d03dfae.png)



Voltar para Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.