Bom dessa vez estou com duas dúvuidas...
A primeira é em relação a este problema:
*Numa certa cultura existem 1000 bactérias em determinado instante. Após 10 minutos, existem 4000.Quantas bactérias existirão em 1 hora, sabendo que elas aumentam através da fórmula P=Po .
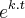 , em que P é o nº de bactérias, t é o tempo em horas e k é a taxa de crescimento?
, em que P é o nº de bactérias, t é o tempo em horas e k é a taxa de crescimento?- - -Eu não sei como calcular a taxa de crescimento, alguém ajuda??O restante do problema eu sei como resolver mas não sei como descubro a taxa.
--------------------------------:D-------------------------:)------------------;)----------------:P--------------XD---------------------------------
*A mortalidade infantil do Senegal está sendo reduzida a uma taxa de 10% ao ano.Quanto tempo levará para que a mortalidade infantil seja reduzida a 50%, sabendo que essa situação pode ser modelada pela função exponencial y=yo.
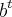
- - -E nessa questão eu não sei como achar um número em anos, se o problema se me fornece as porcentagens de redução
Obrigadaa mais uma vez
;**



![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)