Juros SAC

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

Juros SAC

Regras do fórum
Responder

Juros SAC

Mensagempor carolmds » Qua Mai 08, 2019 09:12

Uma dívida será paga em 24 parcelas semestrais no sistema SAC. Porém, os juros é de 1% ao ano. Para transformar ela ao semestre considero juros simples, 0,5%, ou faço aquela fórmula de taxa equivalente?
carolmds
Novo Usuário
Novo Usuário
 
Mensagens: 1
Registrado em: Ter Mai 07, 2019 19:03
Formação Escolar: PÓS-GRADUAÇÃO
Área/Curso: economia
Andamento: cursando
Voltar ao topo

Re: Juros SAC

Mensagempor Baltuilhe » Seg Mai 13, 2019 02:22

Boa noite!

Faça a fórmula de taxa equivalente se a taxa for simplesmente 1% a.a.. Se for 1% a.a. com capitalização semestral, daí só dividir por 2 e obter a equivalente semestral, mesmo.
Portanto:
\left(1+i_s\right)^2=1+1\%\\ 1+i_s=\sqrt{1+0,01}\\ i_s=\sqrt{1,01}-1\\ i__s\approx 0,4988\%

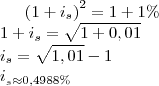
Espero ter ajudado!
Baltuilhe
Usuário Parceiro
Usuário Parceiro
 
Mensagens: 60
Registrado em: Dom Mar 24, 2013 21:16
Formação Escolar: GRADUAÇÃO
Área/Curso: Engenharia Civil
Andamento: formado
Voltar ao topo
Responder

Voltar para Matemática Financeira

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes

 


Tópico Popular

Assunto: Taxa de variação
Autor: felipe_ad - Ter Jun 29, 2010 19:44

Como resolvo uma questao desse tipo:

Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?

A letra (a) consegui resolver e cheguei no resultado correto de \frac{4\pi{r}^{2}}{3}
Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é 1,066\pi

Alguem me ajuda? Agradeço desde já.

Assunto: Taxa de variação
Autor: Elcioschin - Qua Jun 30, 2010 20:47

V = (1/3)*pi*r²*h ----> h = 4r/3

V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³

Derivando:

dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3

Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s

Assunto: Taxa de variação
Autor: Guill - Ter Fev 21, 2012 21:17

Temos que o volume é dado por:

V = \frac{4\pi}{3}r^2


Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

\frac{dV}{dt} = \frac{8\pi.r}{3}.\frac{dr}{dt}


Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:

\frac{dV}{dt} = \frac{8\pi.2}{3}.\frac{2}{10}

\frac{dV}{dt} = \frac{16\pi}{15}

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

Índice do fórum