Provas
Regras do fórum
- Não envie somente enunciados de problemas, informe suas tentativas e dificuldades!
Queremos que a "ajuda" represente um trabalho interativo, pois saber especificar a dúvida exige estudo.
Serão desconsiderados tópicos apenas com enunciados, sem interação. Nosso objetivo não é resolver listas de exercícios;
- Para não haver má interpretação em suas postagens, especialmente na precedência das operações, utilize LaTeX, podendo ser a partir do botão "editor de fórmulas".
Bons estudos!
 por rcompany » Qui Mar 28, 2019 15:15
por rcompany » Qui Mar 28, 2019 15:15
FUVEST 2017 matemática segunda fase com propostas de resolução.
Comentem, corrijam!
M01
Em uma competição de vólei, estão inscritos 5 times.Pelo regulamento, todos os times devem se enfrentar apenas uma vez e, ao final da competição, eles serão classificados pelo número de vitórias. Dois ou mais times com o mesmo número de vitórias terão a mesma classificação. Em cada jogo, os times têm probabilidade

de vencer.
a) Explique por que 2 times não podem empatar na classificação com 4 vitórias cada um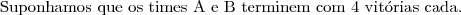
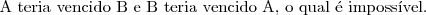 b) Qual é a probabilidade que o primeiro classificado termine a competição com 4 vitórias?
b) Qual é a probabilidade que o primeiro classificado termine a competição com 4 vitórias?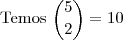



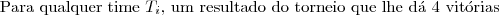


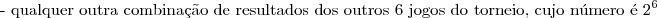

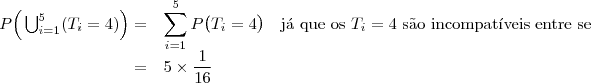 c) Qual é a probabilidade de que os 5 times terminem empatados na classificação?
c) Qual é a probabilidade de que os 5 times terminem empatados na classificação?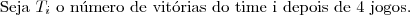
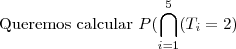 Primeira opção: passar pelo evento complementar
Primeira opção: passar pelo evento complementar. Reduziremos o número de cálculos já que aparecerão eventos incompatíveis (as combinações de
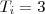
e
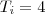
)
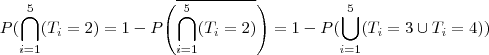
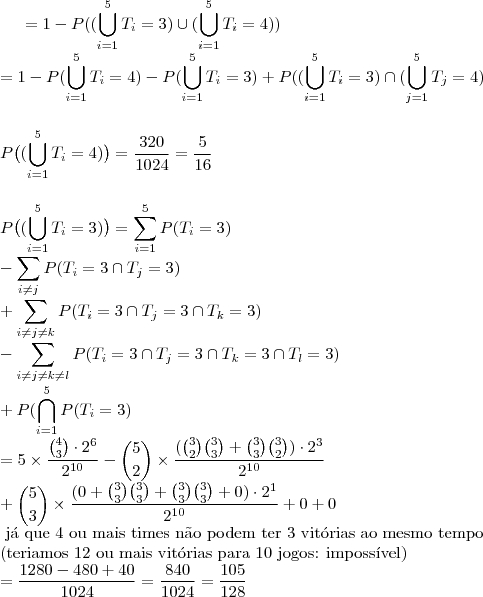
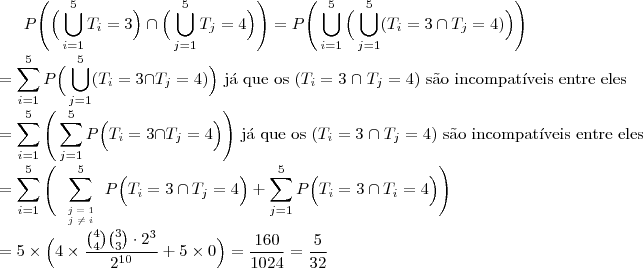
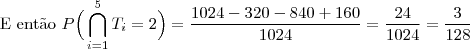 Segunda Opção: usar os resultados possíveis dos jogos de 4 times entre eles
Segunda Opção: usar os resultados possíveis dos jogos de 4 times entre eles
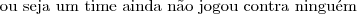


 Terceira opção: calcular diretamente
Terceira opção: calcular diretamente 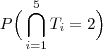
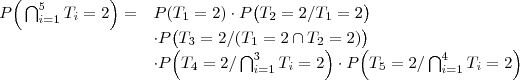
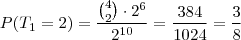
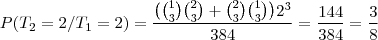
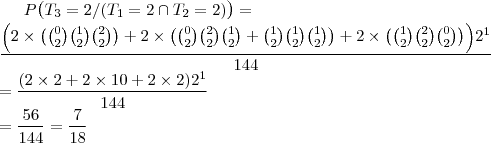
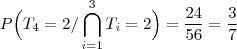

M02
Considere as funções
![f:\;[-\frac{\pi}{2};\frac{\pi}{2}]\rightarrow[-1;1] f:\;[-\frac{\pi}{2};\frac{\pi}{2}]\rightarrow[-1;1]](/latexrender/pictures/75fa245bc12d5cf3cc9b2ce941b79c7e.png)
e
![g:\;[0;\pi]\rightarrow[-1;1] g:\;[0;\pi]\rightarrow[-1;1]](/latexrender/pictures/74aa2ac182c09f10873a477fd03114ca.png)
definidas por
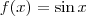
e
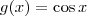
. Sendo f e g bijetoras, existem funções
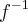
e
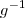
tais que
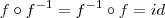
e
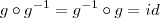
, em que
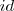
é a função identidade.
a) Para

, mostre que
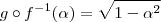
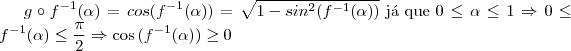
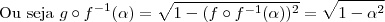
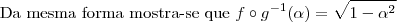
b) Mostre que
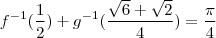
Usar o resultado da primeira questão é um complicação desnecessária quando:
![\begin{array}{rl}f^{-1}(\dfrac{1}{2}) + g^{-1}(\dfrac{\sqrt{6}+\sqrt{2}}{4})=&f^{-1}(\sin{\dfrac{\pi}{6}})+g^{-1}(\dfrac{\sqrt{6}+\sqrt{2}}{4})\\[\bigskipamount]=&\dfrac{\pi}{6} +g^{-1}\Big(\dfrac{1}{\sqrt{2}}\cdot\dfrac{\sqrt{3}}{2}+\dfrac{1}{\sqrt{2}}\cdot\dfrac{1}{2}\Big )\\[\bigskipamount]=&\dfrac{\pi}{6} +g^{-1}\Big(\cos{\dfrac{\pi}{4}}\cos{\dfrac{\pi}{6}}+\sin{\dfrac{\pi}{4}}\sin{\dfrac{\pi}{6}\Big)\\
[\bigskipamount]=&\dfrac{\pi}{6} +g^{-1}\big (\cos{(\dfrac{\pi}{4}-\dfrac{\pi}{6})}\big)\\
[\bigskipamount]=&\dfrac{\pi}{6} +\dfrac{\pi}{12}\\[\bigskipamount]=&\dfrac{\pi}{4}\end{array} \begin{array}{rl}f^{-1}(\dfrac{1}{2}) + g^{-1}(\dfrac{\sqrt{6}+\sqrt{2}}{4})=&f^{-1}(\sin{\dfrac{\pi}{6}})+g^{-1}(\dfrac{\sqrt{6}+\sqrt{2}}{4})\\[\bigskipamount]=&\dfrac{\pi}{6} +g^{-1}\Big(\dfrac{1}{\sqrt{2}}\cdot\dfrac{\sqrt{3}}{2}+\dfrac{1}{\sqrt{2}}\cdot\dfrac{1}{2}\Big )\\[\bigskipamount]=&\dfrac{\pi}{6} +g^{-1}\Big(\cos{\dfrac{\pi}{4}}\cos{\dfrac{\pi}{6}}+\sin{\dfrac{\pi}{4}}\sin{\dfrac{\pi}{6}\Big)\\
[\bigskipamount]=&\dfrac{\pi}{6} +g^{-1}\big (\cos{(\dfrac{\pi}{4}-\dfrac{\pi}{6})}\big)\\
[\bigskipamount]=&\dfrac{\pi}{6} +\dfrac{\pi}{12}\\[\bigskipamount]=&\dfrac{\pi}{4}\end{array}](/latexrender/pictures/0ce6dc6b75247a38575eb4802b96af6b.png)
Ou, usando o resultado de a):
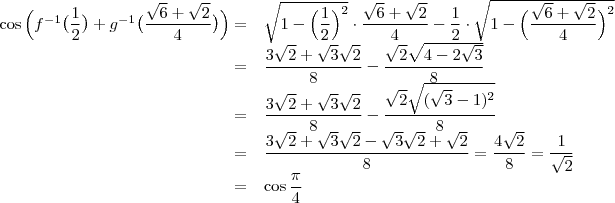
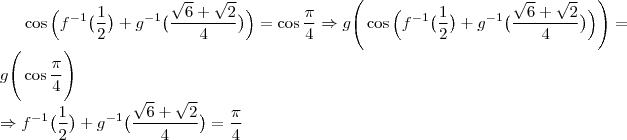
M03
Sejam C um subconjunto não vazio e P um ponto, ambos em um mesmo plano, tais que
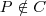
, Diz-se que "P enxerga C sob um ângulo

se

for a medida do menor ângulo com vértice em P que contenha C.
a) Se C for um circulo de raio r , centrado na origem de um plano cartesiano real, determine o lugar geométrico dos pontos que enxergam C sob um ângulo de 60 graus
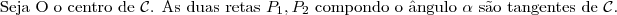

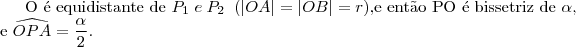
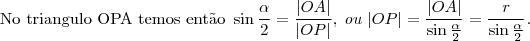
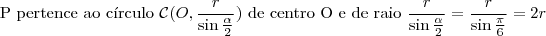
b) Se

for a união dos segmentos
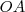
e

em que
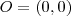
,
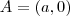
e
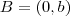
, com
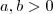
, determine o lugar geométrico dos pontos que enxergam

sob um ângulo de 90 graus.

M04
Considere a sequência
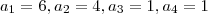
e
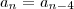
para

. Defina
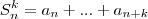
para

, isto é a soma de (k+1) termos consecutivos da sequência começanco no n-ésimo, por exemplo

a) Encontre

tais que

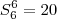
b) Para cada inteiro
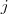
,
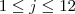
, encontre

tais que
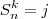
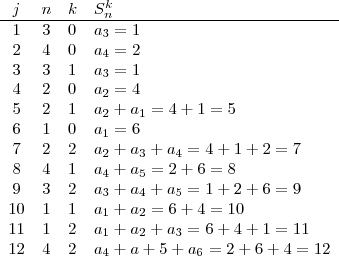
3) Mostre que para qualquer inteiro
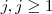
, existem inteiros
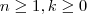
tais que
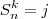

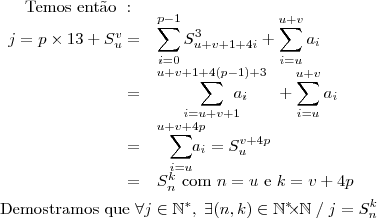
M05
Para responder aos itens a) e b) considere a figura correspondente
a) num tetraedro OABC, os ângulos
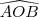
,
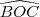
e
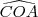
medem 90 graus. Sejam

e

as medidas dos ângulos
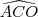
e
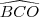
, respetivamente,expresse o cosseno do ângulo
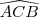
em função de

e




b) Um navio parte do ponto de latitude 0° e de longitude 0°e navega até chagar ao ponto de latitude 45° sul e longitude 45° oeste, seguindo a trajetória que minimiza a distância percorrida. Admita que a terra seja esférica de raio
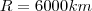
. Qual foi a distância percorrida pelo navio?


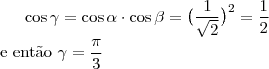
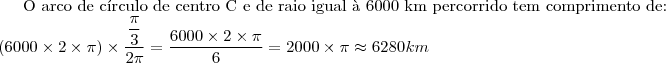
M06
Considere a função real definida por
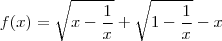
a) Qual é o domínio de f?

![x-\dfrac{1}{x}\geq 0 \Leftrightarrow \dfrac{x^2-1}{x} \geq 0 \Leftrightarrow \left \{\begin{array}{l}x^2-1\geq 0\;se\;x> 0\\x^2-1\leq 0\;se\;x< 0 \end{array} \right\Leftrightarrow \left \{\begin{array}{l}x\geq 1\;se\;x> 0\\x\geq -1\;se\;x< 0 \end{array} \right\Leftrightarrow x\in [-1;0[\cup]1;+\infty[ x-\dfrac{1}{x}\geq 0 \Leftrightarrow \dfrac{x^2-1}{x} \geq 0 \Leftrightarrow \left \{\begin{array}{l}x^2-1\geq 0\;se\;x> 0\\x^2-1\leq 0\;se\;x< 0 \end{array} \right\Leftrightarrow \left \{\begin{array}{l}x\geq 1\;se\;x> 0\\x\geq -1\;se\;x< 0 \end{array} \right\Leftrightarrow x\in [-1;0[\cup]1;+\infty[](/latexrender/pictures/8851b70be126d8ae0d70497f53842dc1.png)
![1-\dfrac{1}{x}\geq 0 \Leftrightarrow 1 \geq \dfrac{1}{x} \Leftrightarrow \left \{\begin{array}{l}x\geq 1\;se\;x> 0\\x\leq 1\;se\;x< 0 \end{array} \right\Leftrightarrow x\in ]-\infty;0[\cup[1;+\infty[ 1-\dfrac{1}{x}\geq 0 \Leftrightarrow 1 \geq \dfrac{1}{x} \Leftrightarrow \left \{\begin{array}{l}x\geq 1\;se\;x> 0\\x\leq 1\;se\;x< 0 \end{array} \right\Leftrightarrow x\in ]-\infty;0[\cup[1;+\infty[](/latexrender/pictures/42358de9232e9b9d8463403170f86b7b.png)
![\mathcal{D}_f = \mathbb{R}^*\;\; \cap\;\; \big ([-1;0[\cup]1;+\infty[\big )\;\; \cap \;\;\big (]-\infty;0[\cup[1;+\infty[\big )=[-1;0[\cup[1;+\infty[ \mathcal{D}_f = \mathbb{R}^*\;\; \cap\;\; \big ([-1;0[\cup]1;+\infty[\big )\;\; \cap \;\;\big (]-\infty;0[\cup[1;+\infty[\big )=[-1;0[\cup[1;+\infty[](/latexrender/pictures/10f9f7c02f2f3590eba1ab45d14f71ed.png)
b) Encontre o(s) valor(es) de

para o(s) qual(is)
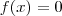
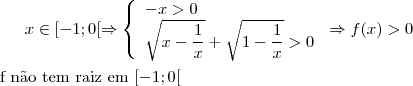


-
rcompany
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Seg Fev 18, 2019 00:57
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: administração
- Andamento: formado
Voltar para Vestibulares
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Polinômios] Prova da fuvest 2ª fase
por vlopagliuca » Qua Dez 12, 2012 15:35
- 1 Respostas
- 2747 Exibições
- Última mensagem por young_jedi

Qua Dez 12, 2012 21:14
Polinômios
-
- Ajuda questão de matemática da fuvest
por gabriela o marengao » Qui Fev 13, 2014 21:22
- 1 Respostas
- 1826 Exibições
- Última mensagem por e8group

Qui Fev 13, 2014 21:57
Funções
-
- Ajuda questão de matemática da fuvest
por gabriela o marengao » Qui Fev 13, 2014 21:24
- 1 Respostas
- 2626 Exibições
- Última mensagem por e8group

Qui Fev 13, 2014 22:08
Lógica
-
- Sød Panda fra Pandora Efterår 2017
por Michael » Qua Jan 31, 2018 03:39
- 0 Respostas
- 0 Exibições
- Última mensagem por Visitante

Qua Dez 31, 1969 22:00
Desafios Médios
-
- Planos de Fase
por marinalcd » Seg Mar 17, 2014 13:19
- 0 Respostas
- 2108 Exibições
- Última mensagem por marinalcd

Seg Mar 17, 2014 13:19
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {

} e B = {

}, então o número de elementos A

B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {

} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {

} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,

Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 de vencer.
de vencer.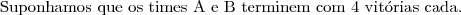
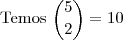



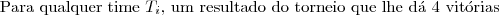


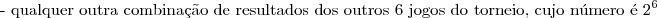

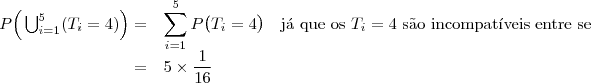
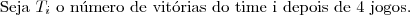
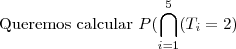
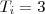 e
e 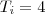 )
)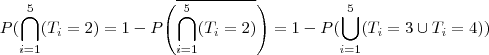
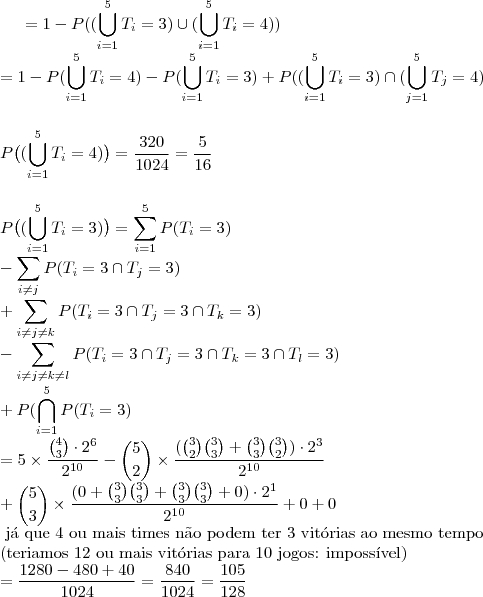
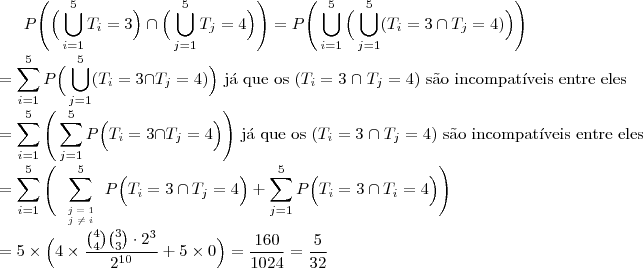
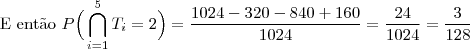

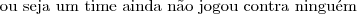


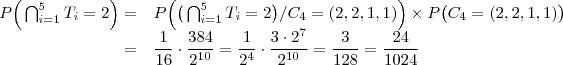
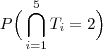
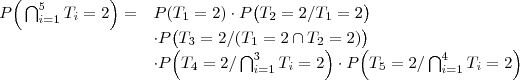
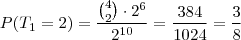
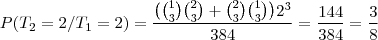
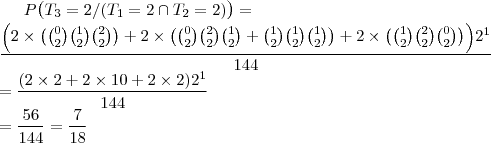
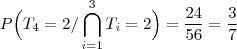

![f:\;[-\frac{\pi}{2};\frac{\pi}{2}]\rightarrow[-1;1] f:\;[-\frac{\pi}{2};\frac{\pi}{2}]\rightarrow[-1;1]](/latexrender/pictures/75fa245bc12d5cf3cc9b2ce941b79c7e.png) e
e ![g:\;[0;\pi]\rightarrow[-1;1] g:\;[0;\pi]\rightarrow[-1;1]](/latexrender/pictures/74aa2ac182c09f10873a477fd03114ca.png) definidas por
definidas por 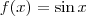 e
e 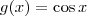 . Sendo f e g bijetoras, existem funções
. Sendo f e g bijetoras, existem funções 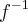 e
e 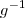 tais que
tais que 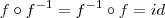 e
e 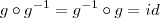 , em que
, em que 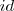 é a função identidade.
é a função identidade. , mostre que
, mostre que 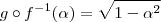
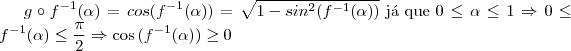
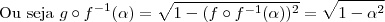
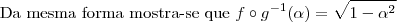
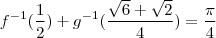
![\begin{array}{rl}f^{-1}(\dfrac{1}{2}) + g^{-1}(\dfrac{\sqrt{6}+\sqrt{2}}{4})=&f^{-1}(\sin{\dfrac{\pi}{6}})+g^{-1}(\dfrac{\sqrt{6}+\sqrt{2}}{4})\\[\bigskipamount]=&\dfrac{\pi}{6} +g^{-1}\Big(\dfrac{1}{\sqrt{2}}\cdot\dfrac{\sqrt{3}}{2}+\dfrac{1}{\sqrt{2}}\cdot\dfrac{1}{2}\Big )\\[\bigskipamount]=&\dfrac{\pi}{6} +g^{-1}\Big(\cos{\dfrac{\pi}{4}}\cos{\dfrac{\pi}{6}}+\sin{\dfrac{\pi}{4}}\sin{\dfrac{\pi}{6}\Big)\\
[\bigskipamount]=&\dfrac{\pi}{6} +g^{-1}\big (\cos{(\dfrac{\pi}{4}-\dfrac{\pi}{6})}\big)\\
[\bigskipamount]=&\dfrac{\pi}{6} +\dfrac{\pi}{12}\\[\bigskipamount]=&\dfrac{\pi}{4}\end{array} \begin{array}{rl}f^{-1}(\dfrac{1}{2}) + g^{-1}(\dfrac{\sqrt{6}+\sqrt{2}}{4})=&f^{-1}(\sin{\dfrac{\pi}{6}})+g^{-1}(\dfrac{\sqrt{6}+\sqrt{2}}{4})\\[\bigskipamount]=&\dfrac{\pi}{6} +g^{-1}\Big(\dfrac{1}{\sqrt{2}}\cdot\dfrac{\sqrt{3}}{2}+\dfrac{1}{\sqrt{2}}\cdot\dfrac{1}{2}\Big )\\[\bigskipamount]=&\dfrac{\pi}{6} +g^{-1}\Big(\cos{\dfrac{\pi}{4}}\cos{\dfrac{\pi}{6}}+\sin{\dfrac{\pi}{4}}\sin{\dfrac{\pi}{6}\Big)\\
[\bigskipamount]=&\dfrac{\pi}{6} +g^{-1}\big (\cos{(\dfrac{\pi}{4}-\dfrac{\pi}{6})}\big)\\
[\bigskipamount]=&\dfrac{\pi}{6} +\dfrac{\pi}{12}\\[\bigskipamount]=&\dfrac{\pi}{4}\end{array}](/latexrender/pictures/0ce6dc6b75247a38575eb4802b96af6b.png)
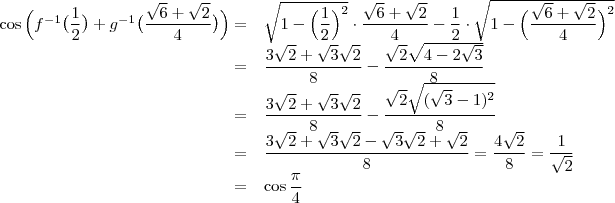
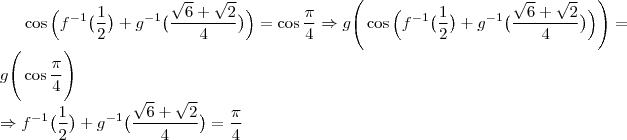
 , Diz-se que "P enxerga C sob um ângulo
, Diz-se que "P enxerga C sob um ângulo  se
se  for a medida do menor ângulo com vértice em P que contenha C.
for a medida do menor ângulo com vértice em P que contenha C.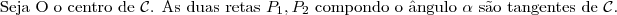

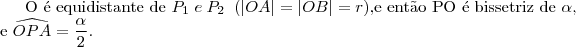
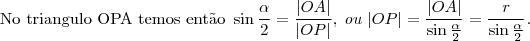
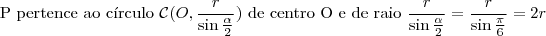
 for a união dos segmentos
for a união dos segmentos 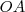 e
e  em que
em que 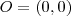 ,
, 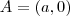 e
e 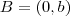 , com
, com 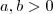 , determine o lugar geométrico dos pontos que enxergam
, determine o lugar geométrico dos pontos que enxergam  sob um ângulo de 90 graus.
sob um ângulo de 90 graus.
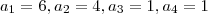 e
e 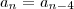 para
para  . Defina
. Defina 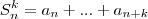 para
para  , isto é a soma de (k+1) termos consecutivos da sequência começanco no n-ésimo, por exemplo
, isto é a soma de (k+1) termos consecutivos da sequência começanco no n-ésimo, por exemplo 
 tais que
tais que 
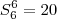
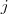 ,
, 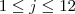 , encontre
, encontre  tais que
tais que 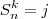
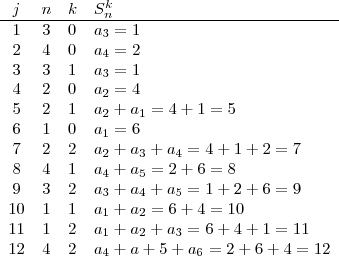
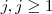 , existem inteiros
, existem inteiros 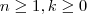 tais que
tais que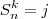

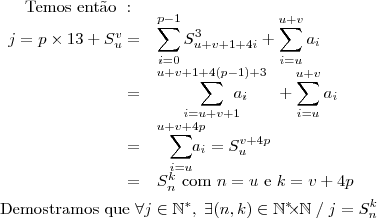
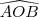 ,
, 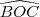 e
e 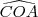 medem 90 graus. Sejam
medem 90 graus. Sejam  e
e  as medidas dos ângulos
as medidas dos ângulos 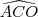 e
e 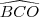 , respetivamente,expresse o cosseno do ângulo
, respetivamente,expresse o cosseno do ângulo 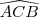 em função de
em função de  e
e 


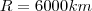 . Qual foi a distância percorrida pelo navio?
. Qual foi a distância percorrida pelo navio?
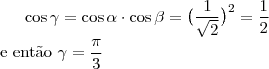
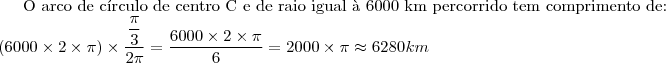
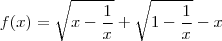

![x-\dfrac{1}{x}\geq 0 \Leftrightarrow \dfrac{x^2-1}{x} \geq 0 \Leftrightarrow \left \{\begin{array}{l}x^2-1\geq 0\;se\;x> 0\\x^2-1\leq 0\;se\;x< 0 \end{array} \right\Leftrightarrow \left \{\begin{array}{l}x\geq 1\;se\;x> 0\\x\geq -1\;se\;x< 0 \end{array} \right\Leftrightarrow x\in [-1;0[\cup]1;+\infty[ x-\dfrac{1}{x}\geq 0 \Leftrightarrow \dfrac{x^2-1}{x} \geq 0 \Leftrightarrow \left \{\begin{array}{l}x^2-1\geq 0\;se\;x> 0\\x^2-1\leq 0\;se\;x< 0 \end{array} \right\Leftrightarrow \left \{\begin{array}{l}x\geq 1\;se\;x> 0\\x\geq -1\;se\;x< 0 \end{array} \right\Leftrightarrow x\in [-1;0[\cup]1;+\infty[](/latexrender/pictures/8851b70be126d8ae0d70497f53842dc1.png)
![1-\dfrac{1}{x}\geq 0 \Leftrightarrow 1 \geq \dfrac{1}{x} \Leftrightarrow \left \{\begin{array}{l}x\geq 1\;se\;x> 0\\x\leq 1\;se\;x< 0 \end{array} \right\Leftrightarrow x\in ]-\infty;0[\cup[1;+\infty[ 1-\dfrac{1}{x}\geq 0 \Leftrightarrow 1 \geq \dfrac{1}{x} \Leftrightarrow \left \{\begin{array}{l}x\geq 1\;se\;x> 0\\x\leq 1\;se\;x< 0 \end{array} \right\Leftrightarrow x\in ]-\infty;0[\cup[1;+\infty[](/latexrender/pictures/42358de9232e9b9d8463403170f86b7b.png)
![\mathcal{D}_f = \mathbb{R}^*\;\; \cap\;\; \big ([-1;0[\cup]1;+\infty[\big )\;\; \cap \;\;\big (]-\infty;0[\cup[1;+\infty[\big )=[-1;0[\cup[1;+\infty[ \mathcal{D}_f = \mathbb{R}^*\;\; \cap\;\; \big ([-1;0[\cup]1;+\infty[\big )\;\; \cap \;\;\big (]-\infty;0[\cup[1;+\infty[\big )=[-1;0[\cup[1;+\infty[](/latexrender/pictures/10f9f7c02f2f3590eba1ab45d14f71ed.png)
 para o(s) qual(is)
para o(s) qual(is) 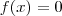
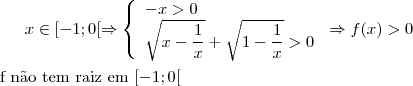



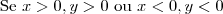
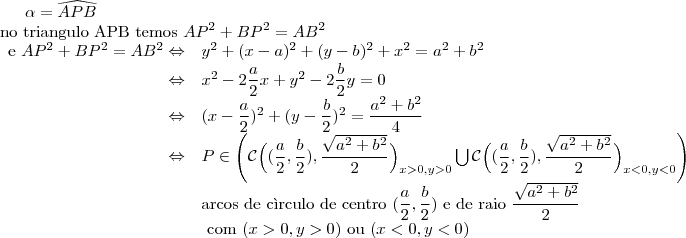
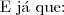
>\dfrac{b^2}{4} \end{array} \right \\[\bigskipamount]&\Rightarrow \big (x-\dfrac{a}{2}\big )^2+\big (y-\dfrac{b}{2}\big )^2>\dfrac{a^2+b^2}{4}\\[\bigskipamount]&\Rightarrow \mathcal{C}\Big((\dfrac{a}{2},\dfrac{b}{2}),\dfrac{\sqrt{a^2+b^2}}{2}\Big)_{x<0,y<0}=\emptyset ,\end{array}\\ \begin{array}{rl} \left \begin{array}{rl}x<0\\y<0 \end{array}\right \} &\Rightarrow \left \{ \begin{array}{rl}(x-\dfrac{a}{2})>\dfrac{a^2}{4}\\[\bigskipamount](y-\dfrac{b}{2})>\dfrac{b^2}{4} \end{array} \right \\[\bigskipamount]&\Rightarrow \big (x-\dfrac{a}{2}\big )^2+\big (y-\dfrac{b}{2}\big )^2>\dfrac{a^2+b^2}{4}\\[\bigskipamount]&\Rightarrow \mathcal{C}\Big((\dfrac{a}{2},\dfrac{b}{2}),\dfrac{\sqrt{a^2+b^2}}{2}\Big)_{x<0,y<0}=\emptyset ,\end{array}\\](/latexrender/pictures/9a0f8b604151253bcffae7ba9e417826.png)
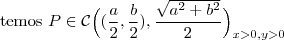

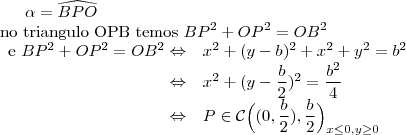
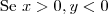
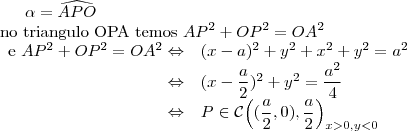
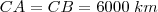
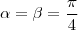

 } e B = {
} e B = { }, então o número de elementos A
}, então o número de elementos A  B é:
B é: