Interseção entre áreas (Integrais)

[thejotta]

A área de A ? B, onde

A={ (x,y) ?R2:0 ? x ? ?/2, 0 ? y ? c o s x }

B={ (x, y) ?R2: 0 < x < ?/2, sin x ? y ? 1}

é igual a:

a)(?2 - 1) /2
b)?2 /2
c)?2 - 1
d)1
e)?2

Não estou conseguindo resolver essa questão, alguém pode me ajudar?

o que eu fiz: Calculei a área de
A = 1
B = ?/2 -1

Sei que o gabarito é letra C. mas não sei como chegar nesse resultado.

[Gebe]

Sempre que possivel faça o desenho!

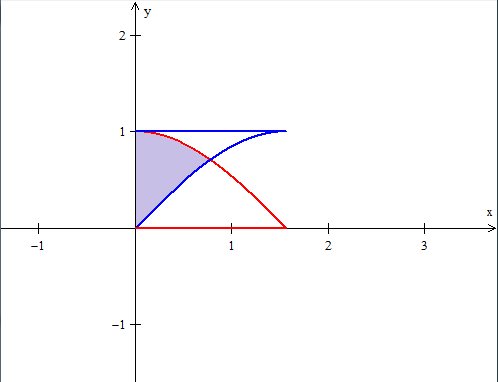
area.png (6.36 KiB) Exibido 11026 vezes

A area destacada é a pedida, portanto precisamos primeiramente achar onde as duas senoides se tocam, ou seja, sen(x) = cos(x).
Neste intervalo a intersecção acontece em pi/4 (ou 45°).

Agora para calcular a area de intersecção podemos calcular a area abaixo do cosseno entre 0 e pi/4 e subtrair a area abaixo do seno entre 0 e pi/4:


Espero ter ajudado, bons estudos.

[thejotta]

Muito obrigado. Agora consegui entender, que Deus te abençoe.

[Gebe]