Determine os valores de
 para os quais det (A-
para os quais det (A- I)=0 sendo A=
I)=0 sendo A=
e I=

a matriz identidade
det=2-1-0 =1

 para os quais det (A-
para os quais det (A- I)=0 sendo A=
I)=0 sendo A=


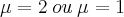 . Pode assumir os dois valores para que
. Pode assumir os dois valores para que 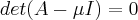 seja atendido. Abaixo segue a resolução.
seja atendido. Abaixo segue a resolução.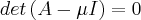
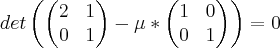
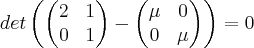
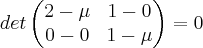
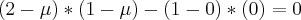
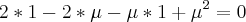

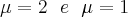 . Nao coloquei a resolução da eq. de 2° grau, mas se precisar é so mandar msg.
. Nao coloquei a resolução da eq. de 2° grau, mas se precisar é so mandar msg.

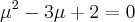 temos:
temos:![\mu=\frac{-b\pm\sqrt[2]{\Delta}}{2a} \mu=\frac{-b\pm\sqrt[2]{\Delta}}{2a}](/latexrender/pictures/1df135ffb0a928cdef029b9a72d4c979.png)

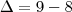
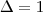
![\mu=\frac{-(-3)\pm\sqrt[2]{1}}{2*1} \mu=\frac{-(-3)\pm\sqrt[2]{1}}{2*1}](/latexrender/pictures/05438fe13d55ffe36a6eaa9498425298.png)
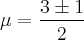

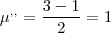








Voltar para Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)