 por ezidia51 » Dom Mar 25, 2018 16:27
por ezidia51 » Dom Mar 25, 2018 16:27
Alguém poderia conferir se este cálculo de procentagem está correto?
Se o raio da base de um cilindro sofrer uma redução de 10% e sua
altura for aumentada em 20% qual será a alteração do volume em % ?
Para calcularmos a porcentagem usamos a fórmula do volume do cilindro
( V= ?.r2..H ) sendo r =1 e H=1
Redução de 10% do raio =0,9
Aumento de 20% na altura =1,2
volume novo .
volume original
O volume novo é V= ?.0, 9.r(original)2 .h(1.2)
O volume original é V= ?.r(original)2 .h(original)
V= = =0,97133 ou 97,13%
?.(1)2.1
?.(0,9)2..1.2
3,14.12.1
3,14.(0,9)2..1.2
Deste modo ,o novo volume é 97,13% = 100%-97,13=2,87%
O cilindro teve o volume reduzido em 2,87% e esta foi a alteração 2,87%
-
ezidia51
- Colaborador Voluntário

-
- Mensagens: 104
- Registrado em: Seg Mar 12, 2018 20:57
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: tecnico em enfermagem
- Andamento: formado
 por Gebe » Dom Mar 25, 2018 18:23
por Gebe » Dom Mar 25, 2018 18:23
Nao consegui entender o que tu fez nesta parte:
ezidia51 escreveu:...
V= = =0,97133 ou 97,13%
?.(1)2.1
?.(0,9)2..1.2
3,14.12.1
3,14.(0,9)2..1.2
O desenvolvimento anterior a ela estava certo sim. A partir dali temos:
O volume novo:

O volume original:
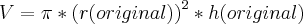
A relação entre os dois volumes (original e novo) nos da a parcela de aumento (ou redução do volume.
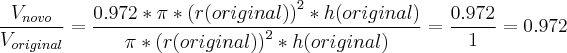
Isso nos diz que o volume novo é 97.2% do valor original, logo houve uma redução volumetrica de (100%-97.2%), ou seja, 2.8%
-
Gebe
- Colaborador Voluntário

-
- Mensagens: 158
- Registrado em: Qua Jun 03, 2015 22:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia eletrica
- Andamento: cursando
 por ezidia51 » Dom Mar 25, 2018 19:21
por ezidia51 » Dom Mar 25, 2018 19:21
-
ezidia51
- Colaborador Voluntário

-
- Mensagens: 104
- Registrado em: Seg Mar 12, 2018 20:57
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: tecnico em enfermagem
- Andamento: formado
Voltar para Aritmética
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Cálculo com porcentagem
por Flavio Antonio » Sex Fev 26, 2010 18:36
- 1 Respostas
- 3216 Exibições
- Última mensagem por MarceloFantini

Sáb Fev 27, 2010 00:28
Matemática Financeira
-
- Calculo com porcentagem
por andersontricordiano » Dom Mai 15, 2011 20:41
- 1 Respostas
- 3428 Exibições
- Última mensagem por carlosalesouza

Dom Mai 15, 2011 21:20
Matemática Financeira
-
- Calculo de porcentagem
por andersontricordiano » Ter Mai 17, 2011 12:36
- 1 Respostas
- 2184 Exibições
- Última mensagem por claudinho

Qua Jun 15, 2011 17:35
Matemática Financeira
-
- [Dificuldade] com cálculo de porcentagem
por rkuguyama » Qui Set 18, 2014 13:36
- 1 Respostas
- 4816 Exibições
- Última mensagem por nakagumahissao

Sáb Set 20, 2014 01:03
Probabilidade
-
- [DESVIO PADRÃO E PORCENTAGEM] CÁLCULO
por scardao » Sáb Jun 14, 2014 16:07
- 0 Respostas
- 3538 Exibições
- Última mensagem por scardao

Sáb Jun 14, 2014 16:07
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



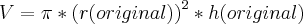
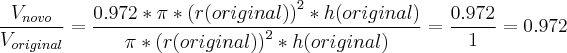

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
