![\sqrt[3]{2,5}.\sqrt[3]{400}=\sqrt[3]{2,5.400}=\sqrt[3]{1000}=\sqrt[3]{2^3.5^3}=2.5=10 \sqrt[3]{2,5}.\sqrt[3]{400}=\sqrt[3]{2,5.400}=\sqrt[3]{1000}=\sqrt[3]{2^3.5^3}=2.5=10](/latexrender/pictures/9197b35c6be452b03c6f8466a09da16b.png) =a-3.b3.c-5
=a-3.b3.c-5LaTeX: \frac{a^2 b^7 c^{-2}}{a^5 b^{-4} c^{-7}}a2b7c?2a5b?4c?7= a^-3.b^5.c^-5
LaTeX: \sqrt{25\%} + 3\%=0,25+0,03=0,5+0,03=0,53 ou 53%
LaTeX: (50\%)^2=(0,5)^2=0,25 = 25

![\sqrt[3]{2,5}.\sqrt[3]{400}=\sqrt[3]{2,5.400}=\sqrt[3]{1000}=\sqrt[3]{2^3.5^3}=2.5=10 \sqrt[3]{2,5}.\sqrt[3]{400}=\sqrt[3]{2,5.400}=\sqrt[3]{1000}=\sqrt[3]{2^3.5^3}=2.5=10](/latexrender/pictures/9197b35c6be452b03c6f8466a09da16b.png) =a-3.b3.c-5
=a-3.b3.c-5
![\sqrt[3]{2,5}.\sqrt[3]{400}=\sqrt[3]{2,5.400}=\sqrt[3]{1000}=\sqrt[3]{2^3.5^3}=2.5=10 \sqrt[3]{2,5}.\sqrt[3]{400}=\sqrt[3]{2,5.400}=\sqrt[3]{1000}=\sqrt[3]{2^3.5^3}=2.5=10](/latexrender/pictures/9197b35c6be452b03c6f8466a09da16b.png)
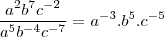

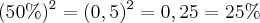
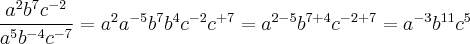
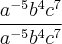 e com isso podemos "cortar" o denominador da expressão.
e com isso podemos "cortar" o denominador da expressão.
















Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes

 .
.
 :
: