 por DarioCViveiros » Qua Fev 21, 2018 17:28
por DarioCViveiros » Qua Fev 21, 2018 17:28
Após uma leitura do livro "Um curso de cálculo - volume 1" de Guidorizzi, decidi verificar se todos os polinômios são contínuos para todo
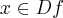
através do uso de
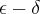
. Gostaria de saber se a minha demonstração está certa e, se não estiver, quais os problemas.
Demonstração:
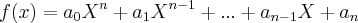 (1)
(1)Onde:
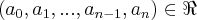
, e
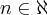
logo,
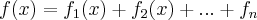
sendo assim,
![(p, f(p)) \in f \Leftrightarrow (p, f(p)) \in {f}_{1}, {f}_{2},..., {f}_{n} \Leftrightarrow \exists (\epsilon>0\rightarrow\delta>0)|\forall x\in {D}_{f} \rightarrow
\exists(I=]a,b[; p \in I)|x\in I\Rightarrow f(p)-\epsilon < f(x) < f(p) + \epsilon (p, f(p)) \in f \Leftrightarrow (p, f(p)) \in {f}_{1}, {f}_{2},..., {f}_{n} \Leftrightarrow \exists (\epsilon>0\rightarrow\delta>0)|\forall x\in {D}_{f} \rightarrow
\exists(I=]a,b[; p \in I)|x\in I\Rightarrow f(p)-\epsilon < f(x) < f(p) + \epsilon](/latexrender/pictures/b5428ff9676b522add714d5ecc83eb6b.png)
com:
![\delta = min[b-p,p+a] \Rightarrow p - \delta < x < p + \delta \delta = min[b-p,p+a] \Rightarrow p - \delta < x < p + \delta](/latexrender/pictures/7dc158336d2e10d06988b41e31d6174b.png)
e:
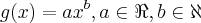
sendo

uma generalização das funções
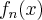
que formam a forma geral de um polinômio (1).
Logo:
![x\in ]a,b[ \Rightarrow x \in ]b-p,p+a[ \Rightarrow p-\delta < x < p + \delta x\in ]a,b[ \Rightarrow x \in ]b-p,p+a[ \Rightarrow p-\delta < x < p + \delta](/latexrender/pictures/e3fe7c48c3db42378d1b0502a8c94b3f.png)
e, para encontrar o intervalo aberto I que torna contínua a função

, toma-se
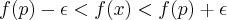
com

, que resulta:
![a{p}^{b}-\epsilon<a{x}^{b}<a{p}^{b}+\epsilon\Rightarrow
\sqrt{\frac{a{p}^{b}-\epsilon}{a}}<x<\sqrt[b]{\frac{a{p}^{b}+\epsilon}{a}} a{p}^{b}-\epsilon<a{x}^{b}<a{p}^{b}+\epsilon\Rightarrow
\sqrt{\frac{a{p}^{b}-\epsilon}{a}}<x<\sqrt[b]{\frac{a{p}^{b}+\epsilon}{a}}](/latexrender/pictures/306ec5b206368af951a3852ead881d80.png)
,
logo:
![I=]\sqrt[b]{\frac{a{p}^{b}-\epsilon}{a}},\sqrt[b]{\frac{a{p}^{b}+\epsilon}{a}}[ I=]\sqrt[b]{\frac{a{p}^{b}-\epsilon}{a}},\sqrt[b]{\frac{a{p}^{b}+\epsilon}{a}}[](/latexrender/pictures/32897c97d27c61ea0118f186a1751d20.png)
o que implica que:
![\exists(\epsilon>0\rightarrow\delta>0)|\forall x\in {D}_{f}\rightarrow\exists(I=]a,b[,p\in I)|x\in I\Rightarrow
f(p)-\epsilon<f(x)<f(p)+\epsilon \exists(\epsilon>0\rightarrow\delta>0)|\forall x\in {D}_{f}\rightarrow\exists(I=]a,b[,p\in I)|x\in I\Rightarrow
f(p)-\epsilon<f(x)<f(p)+\epsilon](/latexrender/pictures/edb731ac9fddebb10e6e8227934da1cf.png)
com:
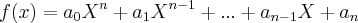 ,
,comprovando que todo polinômio é contínuo

.
Baseie-me aqui nos métodos mostrados no próprio livro, o qual envolve um intervalo aberto no domínio da função, ainda que não tenha encontrado referências a este em outras fontes, como em "Calculus" de Spivak.
Espero receber críticas à minha demonstração em breve, de forma que possa aprimorar o meu conhecimento sobre continuidade. Agradeço desde já.

-
DarioCViveiros
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qua Fev 21, 2018 16:33
- Localização: PI
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Aviso a todos
por Maykids » Qui Jul 14, 2011 02:03
- 2 Respostas
- 1865 Exibições
- Última mensagem por LuizAquino

Qui Jul 14, 2011 15:19
Cálculo: Limites, Derivadas e Integrais
-
- Feliz Natal a todos !!!
por Renato_RJ » Sex Dez 23, 2011 23:27
- 1 Respostas
- 3229 Exibições
- Última mensagem por Neperiano

Ter Jan 03, 2012 21:03
Mensagens Matemáticas
-
- (Fatoração)(UFMG)-Considere o conjunto de todos os ...
por wgf » Qua Mai 29, 2013 19:42
- 1 Respostas
- 9001 Exibições
- Última mensagem por Rafael16

Qua Mai 29, 2013 23:00
Álgebra Elementar
-
- [Integral Imprópria] Definida para todos os ptos
por carol-cvw » Qui Mar 21, 2013 18:10
- 1 Respostas
- 1783 Exibições
- Última mensagem por young_jedi

Sáb Mar 23, 2013 16:57
Cálculo: Limites, Derivadas e Integrais
-
- [Polinômios] Grau do Polinômios e +
por Warioboy » Ter Mai 29, 2012 15:06
- 5 Respostas
- 8378 Exibições
- Última mensagem por Cleyson007

Dom Jun 03, 2012 16:18
Polinômios
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
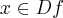 através do uso de
através do uso de 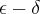 . Gostaria de saber se a minha demonstração está certa e, se não estiver, quais os problemas.
. Gostaria de saber se a minha demonstração está certa e, se não estiver, quais os problemas.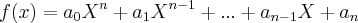 (1)
(1)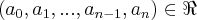 , e
, e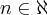
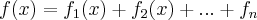
![(p, f(p)) \in f \Leftrightarrow (p, f(p)) \in {f}_{1}, {f}_{2},..., {f}_{n} \Leftrightarrow \exists (\epsilon>0\rightarrow\delta>0)|\forall x\in {D}_{f} \rightarrow
\exists(I=]a,b[; p \in I)|x\in I\Rightarrow f(p)-\epsilon < f(x) < f(p) + \epsilon (p, f(p)) \in f \Leftrightarrow (p, f(p)) \in {f}_{1}, {f}_{2},..., {f}_{n} \Leftrightarrow \exists (\epsilon>0\rightarrow\delta>0)|\forall x\in {D}_{f} \rightarrow
\exists(I=]a,b[; p \in I)|x\in I\Rightarrow f(p)-\epsilon < f(x) < f(p) + \epsilon](/latexrender/pictures/b5428ff9676b522add714d5ecc83eb6b.png)
![\delta = min[b-p,p+a] \Rightarrow p - \delta < x < p + \delta \delta = min[b-p,p+a] \Rightarrow p - \delta < x < p + \delta](/latexrender/pictures/7dc158336d2e10d06988b41e31d6174b.png)
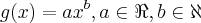
 uma generalização das funções
uma generalização das funções 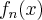 que formam a forma geral de um polinômio (1).
que formam a forma geral de um polinômio (1).![x\in ]a,b[ \Rightarrow x \in ]b-p,p+a[ \Rightarrow p-\delta < x < p + \delta x\in ]a,b[ \Rightarrow x \in ]b-p,p+a[ \Rightarrow p-\delta < x < p + \delta](/latexrender/pictures/e3fe7c48c3db42378d1b0502a8c94b3f.png)
 , toma-se
, toma-se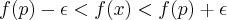 com
com  , que resulta:
, que resulta:![a{p}^{b}-\epsilon<a{x}^{b}<a{p}^{b}+\epsilon\Rightarrow
\sqrt{\frac{a{p}^{b}-\epsilon}{a}}<x<\sqrt[b]{\frac{a{p}^{b}+\epsilon}{a}} a{p}^{b}-\epsilon<a{x}^{b}<a{p}^{b}+\epsilon\Rightarrow
\sqrt{\frac{a{p}^{b}-\epsilon}{a}}<x<\sqrt[b]{\frac{a{p}^{b}+\epsilon}{a}}](/latexrender/pictures/306ec5b206368af951a3852ead881d80.png) ,
,![I=]\sqrt[b]{\frac{a{p}^{b}-\epsilon}{a}},\sqrt[b]{\frac{a{p}^{b}+\epsilon}{a}}[ I=]\sqrt[b]{\frac{a{p}^{b}-\epsilon}{a}},\sqrt[b]{\frac{a{p}^{b}+\epsilon}{a}}[](/latexrender/pictures/32897c97d27c61ea0118f186a1751d20.png)
![\exists(\epsilon>0\rightarrow\delta>0)|\forall x\in {D}_{f}\rightarrow\exists(I=]a,b[,p\in I)|x\in I\Rightarrow
f(p)-\epsilon<f(x)<f(p)+\epsilon \exists(\epsilon>0\rightarrow\delta>0)|\forall x\in {D}_{f}\rightarrow\exists(I=]a,b[,p\in I)|x\in I\Rightarrow
f(p)-\epsilon<f(x)<f(p)+\epsilon](/latexrender/pictures/edb731ac9fddebb10e6e8227934da1cf.png)
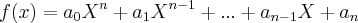 ,
, .
.

