 por orainha » Sex Fev 03, 2017 23:12
por orainha » Sex Fev 03, 2017 23:12
Boas,
Sou novo aqui e venho colocar a minha questão e o que fiz para a tentar resolver, ora bem:
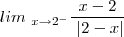
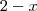
para
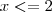
que é o caso
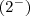
, então
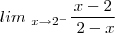
O problema é que não consigo sair da indeterminação. Tenho a solução final de -1, mas preciso de saber como lá chegar
Divisão de polinomios é solução?
Alguém me pode ajudar??
Obrigado.
-
orainha
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Fev 03, 2017 22:51
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Matemática
- Andamento: cursando
 por Alvaro UTFPR » Qui Mar 30, 2017 10:41
por Alvaro UTFPR » Qui Mar 30, 2017 10:41
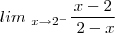
Eu cheguei em uma solução não muito satisfatória, mas pode ajudar.
Se voce tomar conta que o seu x tende a 2 pela esquerda, ou seja , um número menor que 2(ex:1.99) irá perceber que o módulo de |2-x|-{quando x>=0 2-x || quando x<0 -2+x} é sempre positivo quando se aproxima de 2, dessa forma >>|2-x|=2-x, eliminando o módulo.
Depois desse processo
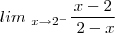
=

= -1
-
Alvaro UTFPR
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qui Mar 30, 2017 10:26
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por orainha » Qui Mar 30, 2017 21:42
por orainha » Qui Mar 30, 2017 21:42
Certo.
Não respondi a este tópico antes. Mas a solução passa por isso mesmo. Colocar o ''-'' em evidencia e trocar os sinais, equivalente a -1.

Ficamos com a solução final de -1.
Grande Abraço e Obrigado.
-
orainha
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Fev 03, 2017 22:51
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [limite] Cancelar denominador
por emanes » Sex Ago 17, 2012 09:34
- 1 Respostas
- 1733 Exibições
- Última mensagem por e8group

Sex Ago 17, 2012 10:22
Cálculo: Limites, Derivadas e Integrais
-
- Limite com raiz de X no denominador
por janainasabidussi » Dom Out 26, 2014 17:42
- 1 Respostas
- 2195 Exibições
- Última mensagem por adauto martins

Seg Out 27, 2014 14:14
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITE] Com a raiz no numerador e denominador!!
por mih123 » Seg Ago 27, 2012 03:52
- 6 Respostas
- 5299 Exibições
- Última mensagem por mih123

Ter Ago 28, 2012 15:09
Cálculo: Limites, Derivadas e Integrais
-
- [Limite]não consigo fazer com que o denominador não de zero.
 por marcosmuscul » Ter Mar 26, 2013 12:52
por marcosmuscul » Ter Mar 26, 2013 12:52
- 2 Respostas
- 1979 Exibições
- Última mensagem por marcosmuscul

Ter Mar 26, 2013 19:48
Cálculo: Limites, Derivadas e Integrais
-
- Limite com raíz cubica sendo o denominador x
por danivelosor » Sáb Mar 28, 2015 21:49
- 1 Respostas
- 2498 Exibições
- Última mensagem por DanielFerreira

Sáb Abr 04, 2015 18:48
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
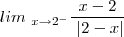
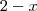 para
para 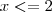 que é o caso
que é o caso 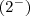 , então
, então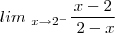


 = -1
= -1