 por Raphaelphtp » Seg Jan 16, 2017 15:33
por Raphaelphtp » Seg Jan 16, 2017 15:33
4) Considerando a função y = lnx e a equação diferencial ordinária x.y’’ + y’ = 0, pode-se afirmar que
:
A.( ) y = lnx é uma solução para a EDO dada no intervalo I = [0, +infinito ).
B.( ) y = lnx é uma solução para a EDO dada no intervalo I = [0, + infinito].
C.( ) y = lnx é uma solução para a EDO dada no intervalo I = [0, + infinito).
D.( ) y = lnx é uma solução para a EDO dada no intervalo I = [– 1, + ).
Pelas minhas contas, deveria ser I = (0,+infinito). com PARENTESES no inicio e no fim, vi que a alternativa A e C, são iguais, será que estou certo? em uma delas deveria ser parenteses no inicio e fim?
onde está escrito +infinito é pq nao consegui por o simbolo.
-
Raphaelphtp
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Ter Dez 20, 2016 10:12
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura Matemática
- Andamento: formado
 por adauto martins » Ter Jan 17, 2017 11:17
por adauto martins » Ter Jan 17, 2017 11:17
faz-se
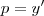
,teremos entao:
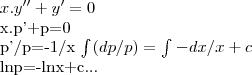
![x.y''+y'=0
x.p'+p=0
p'/p=-1/x
\int_{}^{}(dp/p)=\int_{}^{}-dx/x+c
[tex]y'={e}^{-lnx+c}={e}^{c}.{e}^{-lnx}=k/x...
\int_{}^{}y'=k.\int_{}^{}dx/x+c
y=k.lnx+c...k,c \in \Re... x.y''+y'=0
x.p'+p=0
p'/p=-1/x
\int_{}^{}(dp/p)=\int_{}^{}-dx/x+c
[tex]y'={e}^{-lnx+c}={e}^{c}.{e}^{-lnx}=k/x...
\int_{}^{}y'=k.\int_{}^{}dx/x+c
y=k.lnx+c...k,c \in \Re...](/latexrender/pictures/625a2ad4b95a00d5d300168539fc834b.png)
lnp=-lnx+c...[/tex]
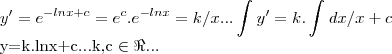
p/x=0
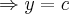
,logo
o intervalo deve conter 0,mas nao é fechado p/ o infinito...
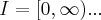
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por Raphaelphtp » Ter Jan 17, 2017 11:42
por Raphaelphtp » Ter Jan 17, 2017 11:42
Grato mais uma vez Adauto

Só não sei se marco A ou C, terei que reclamar sobre essas questões, conteúdo caro e muito mal formulado.
-
Raphaelphtp
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Ter Dez 20, 2016 10:12
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura Matemática
- Andamento: formado
 por adauto martins » Qua Jan 18, 2017 11:03
por adauto martins » Qua Jan 18, 2017 11:03
uma correçao ai meu caro rafael...
mostrei q.
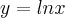
é uma soluçao da equaçao dif. dada,pois o espaço-soluçao,ou famila de curvas é:
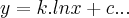
,bom
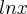
,nao é definida em

,pois
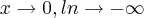
,logo o espaço-soluçao esta definido no
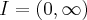
,como vc propos e nao esta nas alternativas,acho precisa buscar um outro livro-texto...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação Diferencial.
por Higor » Seg Fev 21, 2011 13:12
- 4 Respostas
- 12218 Exibições
- Última mensagem por Higor

Seg Fev 21, 2011 14:46
Cálculo: Limites, Derivadas e Integrais
-
- Equaçao diferencial
por romulo39 » Dom Abr 03, 2011 20:58
- 1 Respostas
- 3944 Exibições
- Última mensagem por LuizAquino

Seg Abr 04, 2011 14:39
Cálculo: Limites, Derivadas e Integrais
-
- Equação diferencial
por jacquelline » Qui Mai 17, 2012 11:04
- 2 Respostas
- 2077 Exibições
- Última mensagem por jacquelline

Sáb Mai 19, 2012 20:37
Cálculo: Limites, Derivadas e Integrais
-
- Equação diferencial - 1
por Cleyson007 » Qua Nov 07, 2012 21:09
- 8 Respostas
- 3857 Exibições
- Última mensagem por MarceloFantini

Qui Nov 08, 2012 17:05
Cálculo: Limites, Derivadas e Integrais
-
- Equação diferencial - 2
por Cleyson007 » Qua Nov 07, 2012 21:14
- 1 Respostas
- 1489 Exibições
- Última mensagem por e8group

Qua Nov 14, 2012 10:06
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


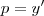 ,teremos entao:
,teremos entao: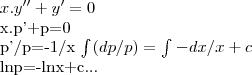
![x.y''+y'=0
x.p'+p=0
p'/p=-1/x
\int_{}^{}(dp/p)=\int_{}^{}-dx/x+c
[tex]y'={e}^{-lnx+c}={e}^{c}.{e}^{-lnx}=k/x...
\int_{}^{}y'=k.\int_{}^{}dx/x+c
y=k.lnx+c...k,c \in \Re... x.y''+y'=0
x.p'+p=0
p'/p=-1/x
\int_{}^{}(dp/p)=\int_{}^{}-dx/x+c
[tex]y'={e}^{-lnx+c}={e}^{c}.{e}^{-lnx}=k/x...
\int_{}^{}y'=k.\int_{}^{}dx/x+c
y=k.lnx+c...k,c \in \Re...](/latexrender/pictures/625a2ad4b95a00d5d300168539fc834b.png)
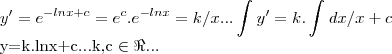
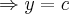 ,logo
,logo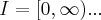


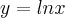 é uma soluçao da equaçao dif. dada,pois o espaço-soluçao,ou famila de curvas é:
é uma soluçao da equaçao dif. dada,pois o espaço-soluçao,ou famila de curvas é: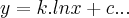 ,bom
,bom 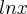 ,nao é definida em
,nao é definida em  ,pois
,pois 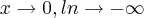 ,logo o espaço-soluçao esta definido no
,logo o espaço-soluçao esta definido no 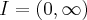 ,como vc propos e nao esta nas alternativas,acho precisa buscar um outro livro-texto...
,como vc propos e nao esta nas alternativas,acho precisa buscar um outro livro-texto...
 .
.



