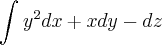 e
e  é a poligonal de vértices A0 = (0,0,0), A1=(1,1,1) e A2=(1,1,0), orientada de A0 para A2.
é a poligonal de vértices A0 = (0,0,0), A1=(1,1,1) e A2=(1,1,0), orientada de A0 para A2.Parametrizei a curva gama, mas ao calcular a integral por partes, cheguei ao resultado 0, porém ao verificar a solução está 5/6. Alguém consegue chegar ao resultado e mostrar-me como?


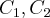 ,
,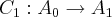 ,temos que:
,temos que: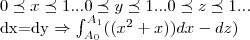
![\int_{0}^{1}({x}^{2}+x)dx-\int_{0}^{1}dz=(({x}^
{3}/3)+({x}^{2}/2)[0,1]-z[0,1]=(1/3)+(1/2)-1=-1/6... \int_{0}^{1}({x}^{2}+x)dx-\int_{0}^{1}dz=(({x}^
{3}/3)+({x}^{2}/2)[0,1]-z[0,1]=(1/3)+(1/2)-1=-1/6...](/latexrender/pictures/6aca2edd13854094e0c12aa3c83bc5a1.png)
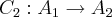 ,temos:
,temos: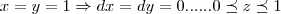 sentido negativo,logo:
sentido negativo,logo:![\int_{{A}_{1}}^{{A}_{2}}(-dz)=[tex]\int_{0}^{1}-dz=\int_{1}^{0}dz=z[1,0]=1... \int_{{A}_{1}}^{{A}_{2}}(-dz)=[tex]\int_{0}^{1}-dz=\int_{1}^{0}dz=z[1,0]=1...](/latexrender/pictures/84ecced62382ad3ceea5983a79cbf3de.png) ...logo o valor da integral sera a soma dos caminhos
...logo o valor da integral sera a soma dos caminhos ,ou seja:
,ou seja: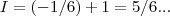
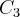 ,ou seja
,ou seja 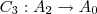 ,teriamos o valor da integral igual a zero,ou seja:
,teriamos o valor da integral igual a zero,ou seja: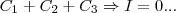 ,fechariamos a linha poligonal...
,fechariamos a linha poligonal...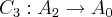
 ,tanto x,y variara negativamente:
,tanto x,y variara negativamente:![\int_{{A}_{2}}^{{A}_{0}}-({x}^{2}+x)dx=-(({x}^{3}/3)+({x}^{2}/2)[(1,1,0),(0,0,0)]=-((1/3)+(1/2)=-5/6... \int_{{A}_{2}}^{{A}_{0}}-({x}^{2}+x)dx=-(({x}^{3}/3)+({x}^{2}/2)[(1,1,0),(0,0,0)]=-((1/3)+(1/2)=-5/6...](/latexrender/pictures/01a69c1f06307e32f654149c7cd4a6fa.png)


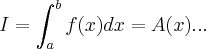 ...metodo da poligonal fechado tem seu uso no calculo de integraçao de variaveis compelexas,calculo do numero de residuos em um compacto qquer...entao é isso...
...metodo da poligonal fechado tem seu uso no calculo de integraçao de variaveis compelexas,calculo do numero de residuos em um compacto qquer...entao é isso...![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)