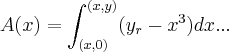por zenildo » Qui Dez 29, 2016 21:10
por adauto martins » Seg Jan 02, 2017 15:22
,onde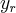 
é a equaçao da reta a ser determinda e 
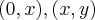serao os pontos de intersecçao da reta com o eixo x,e interseçao da reta com a curva 
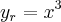,q. sera o intervalo de integraçao...determine-os...por adauto martins » Qui Jan 05, 2017 11:05
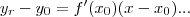,como foi dado o ponto (0,2)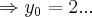 
![(\sqrt[3]{2},2)\in {y}_{r},{x}^{3}](/latexrender/pictures/58e5e36c41810e23134dd266ed180282.png "(\sqrt[3]{2},2)\in {y}_{r},{x}^{3}")
,logo a equaçao da reta tangente sera:![{y}_{r}-2=f'(\sqrt[3]{2})(x-\sqrt[3]{2})...](/latexrender/pictures/0b6112b3bcce2ff7b5bda5398407d76c.png "{y}_{r}-2=f'(\sqrt[3]{2})(x-\sqrt[3]{2})...")
os pontos onde 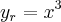,serao os limites de integraçao da integraçao em questao:![3.(\sqrt[3]{2})^{2}).(x-\sqrt[3]{2})+2={x}^{3}\Rightarrow {x}^{3}-3.(\sqrt[3]{2})^{2}(x-\sqrt[3]{2})-2=0\Rightarrow
{x}^{3}-3.(\sqrt[3]{2})^{2})x+(3.\sqrt[3]{2}-2)=0](/latexrender/pictures/7cc98a7e379c84a6a628982bb0c0ece8.png "3.(\sqrt[3]{2})^{2}).(x-\sqrt[3]{2})+2={x}^{3}\Rightarrow {x}^{3}-3.(\sqrt[3]{2})^{2}(x-\sqrt[3]{2})-2=0\Rightarrow
{x}^{3}-3.(\sqrt[3]{2})^{2})x+(3.\sqrt[3]{2}-2)=0")
,ai agora é resolver essa equaçao de terceiro grau...Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
o ângulo entre o eixo horizontal e o afixo 
. O triângulo é retângulo com catetos 
e 
, tal que 
. Seja 
o ângulo complementar. Então 
. Como 
, o ângulo que o afixo 
formará com a horizontal será , mas negativo pois tem de ser no quarto quadrante. Se 
, então 
. Como módulo é um: 
.
.