Eu tenho um exercício que fiquei em dúvida, primeiramente, e aguardarei uma ajuda para a resolução. É o seguinte:
Prove que f(x) = x³ é contínua em p = 2
f(2) = 2³ = 8
Bom, por definição, para todo E > 0 , existe d > 0 tal que |x-2| < d => |f(x)-f(2)| < E .
Desenvolvendo |f(x)-f(2)| < E => |x^3-8| < E => |x^3-2^3| < E => |(x-2)*(x^2+2x+4)| < E => |x-2|*|x^2+2x+4| < E
Daí em diante não sei o que exatamente fazer. Por um livro, descobri que tenho que limitar |x^2+2x+4| porém não sei como fazer isto.
Obrigado a Todos! Bons Estudos!

Obs: E: epsilon e d: delta


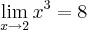 ...no formalismo:
...no formalismo: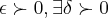 ,tal q.
,tal q. 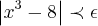 ...
... é raiz do polinomio
é raiz do polinomio 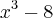 ,logo
,logo 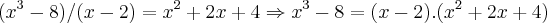 ...
... ,nao tem raizes reais,pois
,nao tem raizes reais,pois 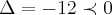 ,entao nao temos como reduzir o seu grau p/valores reais...logo:
,entao nao temos como reduzir o seu grau p/valores reais...logo: ...
... ,desiqualdade triangular
,desiqualdade triangular ...portanto:
...portanto: ,aqui tbem a des.triangular...
,aqui tbem a des.triangular...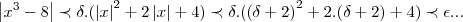
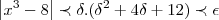 ...pela def. p/um
...pela def. p/um  dado existe pelo um
dado existe pelo um 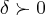 ,o qual procuramos o menor,ou seja
,o qual procuramos o menor,ou seja ![\delta=min[{\delta}_{1},{\delta}_{2},...] \delta=min[{\delta}_{1},{\delta}_{2},...]](/latexrender/pictures/f2a9587965729748f48d2cae0c7f11ba.png) ...geralmente,e o mais correto é tomarmos
...geralmente,e o mais correto é tomarmos 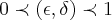 ...logo se tomarmos um num.
...logo se tomarmos um num.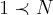 ,podemos ter:
,podemos ter: ...o correto mesmo era resolver a inequaçao
...o correto mesmo era resolver a inequaçao 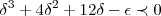 e encontrar o menor
e encontrar o menor 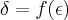 ,mas o exposto acima esta tbem correto...
,mas o exposto acima esta tbem correto...
 o menor
o menor  possivel...ai escreve-se dessa forma
possivel...ai escreve-se dessa forma ![\delta=min[{\delta}_{1},{\delta}_{2}...] \delta=min[{\delta}_{1},{\delta}_{2}...]](/latexrender/pictures/00a6880ee6c56acc6f4110639dfba122.png) ,min[...] toma a conotaçao de menor dos deltas possiveis...
,min[...] toma a conotaçao de menor dos deltas possiveis... em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.