 por p1a2u3lo » Dom Set 18, 2016 11:08
por p1a2u3lo » Dom Set 18, 2016 11:08
Mostrar que a transforma�cão linear A : R2 R3 A(x; y) = (x + y, x - y, y) �e injetiva e
obter uma inversa �a esquerda linear.
-
p1a2u3lo
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Set 18, 2016 10:50
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por adauto martins » Qua Jan 11, 2017 14:47
por adauto martins » Qua Jan 11, 2017 14:47
para que
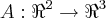
,teremos q. ter
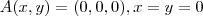
...
de fato,
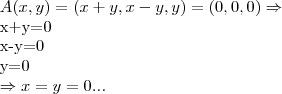
para se ter uma inversa,qquer q. seja a multiplicaçao(a direita ou esquerda),deve-se mostrar q.

é sobrejetiva...
seja
![v=(a.(x+y),b(x-y),c.y)=x.(a+b)+y.(a-b+c)\Rightarrow [a(1,1,0),b(1,-1,0),c(0,0,1)] v=(a.(x+y),b(x-y),c.y)=x.(a+b)+y.(a-b+c)\Rightarrow [a(1,1,0),b(1,-1,0),c(0,0,1)]](/latexrender/pictures/801c93fa2f623d04fad86b588b4d0abb.png)
é uma base p/ IM(A)...logo dim(IM)=3...A é sobrejetiva....portanto admite inversa...entao:
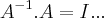
...calcule
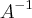
,como exercicio...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Qui Jan 12, 2017 12:00
por adauto martins » Qui Jan 12, 2017 12:00
uma correçao:
a transf.
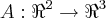
,nao é sobrejetiva,pois:
![v=(x+y,x-y,y)=x(1,1,0)+y(1,-1,0)\Rightarrow [(1,1,0),(1,-1,0)] v=(x+y,x-y,y)=x(1,1,0)+y(1,-1,0)\Rightarrow [(1,1,0),(1,-1,0)]](/latexrender/pictures/15eb8601117c21235dade0d4edb36e70.png)
é uma base de IM(A),logo
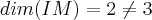
,portanto nao é sobrejetiva...
logo admite,por ser injetiva somente multiplicaçao á esquerda de A...
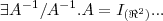
...
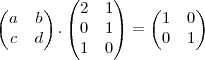
bom ai agora é achar os valores de a,b,c,d...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Transformação Linear] Nucleo e Imagem, ache a transformaçao
por vualas » Qua Nov 07, 2012 00:37
- 2 Respostas
- 4251 Exibições
- Última mensagem por adauto martins

Qui Dez 15, 2016 11:12
Álgebra Linear
-
- [Algebra Linear] - Composição de transformação Linear
por aligames321 » Ter Dez 04, 2012 23:53
- 1 Respostas
- 10530 Exibições
- Última mensagem por young_jedi

Qua Dez 05, 2012 12:45
Álgebra Linear
-
- Álgebra Linear -Transformação linear- Isomorfismo
por anapaulasql » Ter Jan 27, 2015 22:08
- 1 Respostas
- 11563 Exibições
- Última mensagem por adauto martins

Ter Mar 29, 2016 13:15
Álgebra Linear
-
- [Álgebra Linear] Transformação Linear Idenpotente
por Zubumafu67 » Ter Nov 17, 2020 11:38
- 0 Respostas
- 13605 Exibições
- Última mensagem por Zubumafu67

Ter Nov 17, 2020 11:38
Álgebra Linear
-
- [Álgebra Linear] Transformação linear
por Debby » Dom Mai 27, 2012 12:17
- 2 Respostas
- 9145 Exibições
- Última mensagem por Debby

Dom Mai 27, 2012 20:27
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



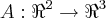 ,teremos q. ter
,teremos q. ter 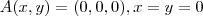 ...
...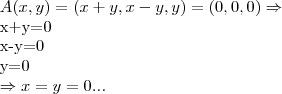
 é sobrejetiva...
é sobrejetiva...![v=(a.(x+y),b(x-y),c.y)=x.(a+b)+y.(a-b+c)\Rightarrow [a(1,1,0),b(1,-1,0),c(0,0,1)] v=(a.(x+y),b(x-y),c.y)=x.(a+b)+y.(a-b+c)\Rightarrow [a(1,1,0),b(1,-1,0),c(0,0,1)]](/latexrender/pictures/801c93fa2f623d04fad86b588b4d0abb.png) é uma base p/ IM(A)...logo dim(IM)=3...A é sobrejetiva....portanto admite inversa...entao:
é uma base p/ IM(A)...logo dim(IM)=3...A é sobrejetiva....portanto admite inversa...entao: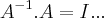 ...calcule
...calcule 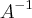 ,como exercicio...
,como exercicio...
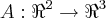 ,nao é sobrejetiva,pois:
,nao é sobrejetiva,pois:![v=(x+y,x-y,y)=x(1,1,0)+y(1,-1,0)\Rightarrow [(1,1,0),(1,-1,0)] v=(x+y,x-y,y)=x(1,1,0)+y(1,-1,0)\Rightarrow [(1,1,0),(1,-1,0)]](/latexrender/pictures/15eb8601117c21235dade0d4edb36e70.png) é uma base de IM(A),logo
é uma base de IM(A),logo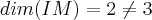 ,portanto nao é sobrejetiva...
,portanto nao é sobrejetiva...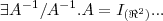 ...
...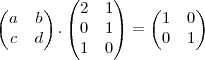


 .
.



