 por adauto martins » Sex Jul 15, 2016 14:48
por adauto martins » Sex Jul 15, 2016 14:48
mostre que:
![({x}_{1}+{x}_{2}+...+{x}_{k})/k\geq \sqrt[k]{({x}_{1}.{x}_{2}.....{x}_{k})} ({x}_{1}+{x}_{2}+...+{x}_{k})/k\geq \sqrt[k]{({x}_{1}.{x}_{2}.....{x}_{k})}](/latexrender/pictures/976e752b1029475407a343e64b08f424.png)
,onde
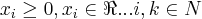
...
soluçao:
vamos tomar
![{A}_{k}=({x}_{1}+...+{x}_{k})/k...{G}_{k}=\sqrt[k]{({x}_{1}...{x}_{k}} {A}_{k}=({x}_{1}+...+{x}_{k})/k...{G}_{k}=\sqrt[k]{({x}_{1}...{x}_{k}}](/latexrender/pictures/a10c9338979f7c016248e98d37b8b432.png)
,segue q.:
![{A}_{1}\geq {G}_{1}({x}_{1}\geq {x}_{1})...{A}_{2}\geq {G}_{2}(({x}_{1}+{x}_{2})/2\geq \sqrt[]{({x}_{1}.{x}_{2})}) {A}_{1}\geq {G}_{1}({x}_{1}\geq {x}_{1})...{A}_{2}\geq {G}_{2}(({x}_{1}+{x}_{2})/2\geq \sqrt[]{({x}_{1}.{x}_{2})})](/latexrender/pictures/ff1ecfdb44b6842a944bc1e69d4b0fb4.png)
,prove isso!...tomaremos entao:
![({A}_{k}+{G}_{k})/2\geq \sqrt[]{({A}_{k}.{G}_{k})} ({A}_{k}+{G}_{k})/2\geq \sqrt[]{({A}_{k}.{G}_{k})}](/latexrender/pictures/cc25d6feb6f5966e58dd51262d6de7f7.png)
[Unparseable or potentially dangerous latex formula. Error 2 ]
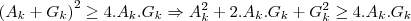
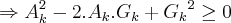
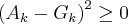
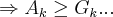
,pois se tomarmos

,contaria a condiçao de
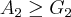
...logo,
![({x}_{1}+...+{x}_{k})/k\geq \sqrt[k]{({x}_{1}....{x}_{k})} ({x}_{1}+...+{x}_{k})/k\geq \sqrt[k]{({x}_{1}....{x}_{k})}](/latexrender/pictures/a23374e1a6641565b8e0038c12cfdb8e.png)
...cqd...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Teoria dos Números
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- exercicio resolvido
por adauto martins » Qua Jul 20, 2016 18:35
- 0 Respostas
- 31782 Exibições
- Última mensagem por adauto martins

Qua Jul 20, 2016 18:35
Cálculo: Limites, Derivadas e Integrais
-
- exercicio resolvido
por adauto martins » Ter Jul 26, 2016 17:43
- 0 Respostas
- 22016 Exibições
- Última mensagem por adauto martins

Ter Jul 26, 2016 17:43
Cálculo: Limites, Derivadas e Integrais
-
- exercicio resolvido
por adauto martins » Sáb Ago 13, 2016 11:28
- 0 Respostas
- 17065 Exibições
- Última mensagem por adauto martins

Sáb Ago 13, 2016 11:28
Teoria dos Números
-
- exercicio resolvido
por adauto martins » Sex Out 18, 2019 14:29
- 2 Respostas
- 22851 Exibições
- Última mensagem por adauto martins

Sex Out 18, 2019 15:42
Trigonometria
-
- exercicio resolvido
por adauto martins » Sáb Out 19, 2019 21:12
- 2 Respostas
- 24343 Exibições
- Última mensagem por adauto martins

Sáb Out 19, 2019 23:51
Aritmética
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![({x}_{1}+{x}_{2}+...+{x}_{k})/k\geq \sqrt[k]{({x}_{1}.{x}_{2}.....{x}_{k})} ({x}_{1}+{x}_{2}+...+{x}_{k})/k\geq \sqrt[k]{({x}_{1}.{x}_{2}.....{x}_{k})}](/latexrender/pictures/976e752b1029475407a343e64b08f424.png) ,onde
,onde 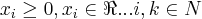 ...
...![{A}_{k}=({x}_{1}+...+{x}_{k})/k...{G}_{k}=\sqrt[k]{({x}_{1}...{x}_{k}} {A}_{k}=({x}_{1}+...+{x}_{k})/k...{G}_{k}=\sqrt[k]{({x}_{1}...{x}_{k}}](/latexrender/pictures/a10c9338979f7c016248e98d37b8b432.png) ,segue q.:
,segue q.:![{A}_{1}\geq {G}_{1}({x}_{1}\geq {x}_{1})...{A}_{2}\geq {G}_{2}(({x}_{1}+{x}_{2})/2\geq \sqrt[]{({x}_{1}.{x}_{2})}) {A}_{1}\geq {G}_{1}({x}_{1}\geq {x}_{1})...{A}_{2}\geq {G}_{2}(({x}_{1}+{x}_{2})/2\geq \sqrt[]{({x}_{1}.{x}_{2})})](/latexrender/pictures/ff1ecfdb44b6842a944bc1e69d4b0fb4.png) ,prove isso!...tomaremos entao:
,prove isso!...tomaremos entao:![({A}_{k}+{G}_{k})/2\geq \sqrt[]{({A}_{k}.{G}_{k})} ({A}_{k}+{G}_{k})/2\geq \sqrt[]{({A}_{k}.{G}_{k})}](/latexrender/pictures/cc25d6feb6f5966e58dd51262d6de7f7.png) [Unparseable or potentially dangerous latex formula. Error 2 ]
[Unparseable or potentially dangerous latex formula. Error 2 ]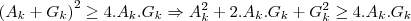
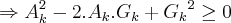
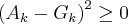
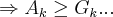 ,pois se tomarmos
,pois se tomarmos  ,contaria a condiçao de
,contaria a condiçao de 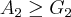 ...logo,
...logo,![({x}_{1}+...+{x}_{k})/k\geq \sqrt[k]{({x}_{1}....{x}_{k})} ({x}_{1}+...+{x}_{k})/k\geq \sqrt[k]{({x}_{1}....{x}_{k})}](/latexrender/pictures/a23374e1a6641565b8e0038c12cfdb8e.png) ...cqd...
...cqd...
![({x}_{1}+{x}_{2}+...+{x}_{k})/k\geq \sqrt[k]{({x}_{1}.{x}_{2}.....{x}_{k})} ({x}_{1}+{x}_{2}+...+{x}_{k})/k\geq \sqrt[k]{({x}_{1}.{x}_{2}.....{x}_{k})}](/latexrender/pictures/976e752b1029475407a343e64b08f424.png) ,onde
,onde 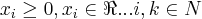 ...
...![{A}_{k}=({x}_{1}+...+{x}_{k})/k...{G}_{k}=\sqrt[k]{({x}_{1}...{x}_{k}} {A}_{k}=({x}_{1}+...+{x}_{k})/k...{G}_{k}=\sqrt[k]{({x}_{1}...{x}_{k}}](/latexrender/pictures/a10c9338979f7c016248e98d37b8b432.png) ,segue q.:
,segue q.:![{A}_{1}\geq {G}_{1}({x}_{1}\geq {x}_{1})...{A}_{2}\geq {G}_{2}(({x}_{1}+{x}_{2})/2\geq \sqrt[]{({x}_{1}.{x}_{2})}) {A}_{1}\geq {G}_{1}({x}_{1}\geq {x}_{1})...{A}_{2}\geq {G}_{2}(({x}_{1}+{x}_{2})/2\geq \sqrt[]{({x}_{1}.{x}_{2})})](/latexrender/pictures/ff1ecfdb44b6842a944bc1e69d4b0fb4.png) ,prove isso!...tomaremos entao:
,prove isso!...tomaremos entao:![({A}_{k}+{G}_{k})/2\geq \sqrt[]{({A}_{k}.{G}_{k})} ({A}_{k}+{G}_{k})/2\geq \sqrt[]{({A}_{k}.{G}_{k})}](/latexrender/pictures/cc25d6feb6f5966e58dd51262d6de7f7.png) [Unparseable or potentially dangerous latex formula. Error 2 ]
[Unparseable or potentially dangerous latex formula. Error 2 ]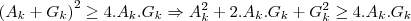
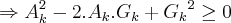
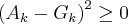
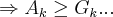 ,pois se tomarmos
,pois se tomarmos  ,contaria a condiçao de
,contaria a condiçao de 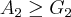 ...logo,
...logo,![({x}_{1}+...+{x}_{k})/k\geq \sqrt[k]{({x}_{1}....{x}_{k})} ({x}_{1}+...+{x}_{k})/k\geq \sqrt[k]{({x}_{1}....{x}_{k})}](/latexrender/pictures/a23374e1a6641565b8e0038c12cfdb8e.png) ...cqd...
...cqd...
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)