 por HenriqueGS » Qui Jun 09, 2016 15:50
por HenriqueGS » Qui Jun 09, 2016 15:50
Uma equação da superfície de uma montanha é z = 1200 - 3x² - 2y², onde a distância é medida em metros. Um alpinista está no ponto correspondente a (-10; 5; 850). A direção que tem maior declividade é dada por qual vetor?
Preciso do desenvolvimento.
-
HenriqueGS
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Dom Jun 05, 2016 20:00
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por adauto martins » Ter Jun 14, 2016 12:30
por adauto martins » Ter Jun 14, 2016 12:30
meu caro henrique ja resolvi esse problema antes,a alguns posts anteriores...minha resposta é essa
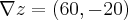
q. é o vetror gradiente da funçao q. da a direçao de maior declividade...vou adequa-la as resposta q. estao la:
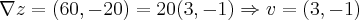
![{u}_{v}=v/\left|v \right|=(3,-1)/\sqrt[]{({3})^{2}+{(-1)}^{2}}=(3,-1)/\sqrt[]{10}\Rightarrow {u}_{v}=(3/\sqrt[]{10},-1/\sqrt[]{10})=(3\sqrt[]{10}/10,-\sqrt[]{10}/10)=3\sqrt[]{10}/10i-\sqrt[]{10}/10j {u}_{v}=v/\left|v \right|=(3,-1)/\sqrt[]{({3})^{2}+{(-1)}^{2}}=(3,-1)/\sqrt[]{10}\Rightarrow {u}_{v}=(3/\sqrt[]{10},-1/\sqrt[]{10})=(3\sqrt[]{10}/10,-\sqrt[]{10}/10)=3\sqrt[]{10}/10i-\sqrt[]{10}/10j](/latexrender/pictures/03db8b63b84b03c76b137dee32fe7d8d.png)
...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [CURVAS] ângulo entre vetor tangente e vetor posição
por inkz » Ter Nov 20, 2012 01:24
- 5 Respostas
- 4918 Exibições
- Última mensagem por LuannLuna

Qui Nov 29, 2012 15:05
Cálculo: Limites, Derivadas e Integrais
-
- [Curvas] Encontrar o vetor posição dado vetor aceleração
 por amigao » Sex Mai 09, 2014 16:37
por amigao » Sex Mai 09, 2014 16:37
- 1 Respostas
- 2091 Exibições
- Última mensagem por Russman

Sex Mai 09, 2014 17:25
Geometria Analítica
-
- [Vetor diretor] Encontrando um vetor diretor
por amigao » Sex Mai 17, 2013 13:19
- 2 Respostas
- 8396 Exibições
- Última mensagem por amigao

Sáb Mai 18, 2013 20:12
Geometria Analítica
-
- Vetor
por cristina » Ter Mai 11, 2010 09:54
- 2 Respostas
- 1983 Exibições
- Última mensagem por cristina

Ter Mai 11, 2010 18:22
Geometria Analítica
-
- Vetor
por CarolMarques » Seg Jul 23, 2012 18:48
- 1 Respostas
- 3235 Exibições
- Última mensagem por LuizAquino

Seg Jul 23, 2012 19:54
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



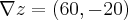 q. é o vetror gradiente da funçao q. da a direçao de maior declividade...vou adequa-la as resposta q. estao la:
q. é o vetror gradiente da funçao q. da a direçao de maior declividade...vou adequa-la as resposta q. estao la: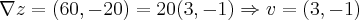
![{u}_{v}=v/\left|v \right|=(3,-1)/\sqrt[]{({3})^{2}+{(-1)}^{2}}=(3,-1)/\sqrt[]{10}\Rightarrow {u}_{v}=(3/\sqrt[]{10},-1/\sqrt[]{10})=(3\sqrt[]{10}/10,-\sqrt[]{10}/10)=3\sqrt[]{10}/10i-\sqrt[]{10}/10j {u}_{v}=v/\left|v \right|=(3,-1)/\sqrt[]{({3})^{2}+{(-1)}^{2}}=(3,-1)/\sqrt[]{10}\Rightarrow {u}_{v}=(3/\sqrt[]{10},-1/\sqrt[]{10})=(3\sqrt[]{10}/10,-\sqrt[]{10}/10)=3\sqrt[]{10}/10i-\sqrt[]{10}/10j](/latexrender/pictures/03db8b63b84b03c76b137dee32fe7d8d.png) ...
...