 por correiomar » Seg Set 07, 2009 23:08
por correiomar » Seg Set 07, 2009 23:08
num triangulo ABC sendo I o incentro deste triangulo e sendo o angulo BIC=8x e A=x determine x.
to arrancando meus cabelos
problema de setima serie entao a resoluçao deve ser simples sem muitas variaveis...
aguardo a ajuda
x=12
-
correiomar
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Seg Set 07, 2009 22:58
- Formação Escolar: ENSINO FUNDAMENTAL I
- Área/Curso: nada
- Andamento: cursando
 por Molina » Ter Set 08, 2009 19:27
por Molina » Ter Set 08, 2009 19:27
correiomar escreveu:num triangulo ABC sendo I o incentro deste triangulo e sendo o angulo BIC=8x e A=x determine x.
to arrancando meus cabelos
problema de setima serie entao a resoluçao deve ser simples sem muitas variaveis...
aguardo a ajuda
x=12
Boa tarde, amigo.
Infelizmente não vou conseguir fazer o desenho para te mostrar como deduzi a solução.
Como o incentro é o encontro das bicetrizes de cada ângulo, o ângulo BIC é formado por duas bicetrizes, ou seja, ele divide o ângulo e o ângulo C pela metade. Desta forma, iria formar um novo triângulo dentro do triângulo ABC, o triângulo BIC que teria como soma dos ângulos os seguintes dados:
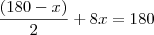
Este
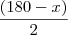
veio da soma da metade dos ângulos B e C, o
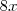
veio do ângulo BIC (enunciado) e 180 é a soma dos ângulos internos de um triângulo. Sendo assim:



Bom estudo,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por correiomar » Ter Set 08, 2009 21:47
por correiomar » Ter Set 08, 2009 21:47
nao entendi a formula 180-x dividido por dois
fiquei intrigado mais com o x
aguardo
-
correiomar
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Seg Set 07, 2009 22:58
- Formação Escolar: ENSINO FUNDAMENTAL I
- Área/Curso: nada
- Andamento: cursando
 por Molina » Qua Set 09, 2009 00:20
por Molina » Qua Set 09, 2009 00:20
correiomar escreveu:nao entendi a formula 180-x dividido por dois
fiquei intrigado mais com o x
aguardo
Boa noite, amigo.
Vamos lá.
180° é a soma dos ângulos internos do triângulo ABC.
Como o ângulo A vale

(enunciado), o ângulo B mais o ângulo C vale
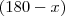
. Certo até aqui?
É dividido por 2, pois estamos pegando a bicetriz destes ângulos (ou seja, a metade).
Faça o desenho com os dados do enunciado que fica fácil de ver isso.
Fico a disposição para maiores informações.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por correiomar » Qua Set 09, 2009 21:11
por correiomar » Qua Set 09, 2009 21:11
valeu entendi
so trabalho molina
-
correiomar
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Seg Set 07, 2009 22:58
- Formação Escolar: ENSINO FUNDAMENTAL I
- Área/Curso: nada
- Andamento: cursando
 por Hazengard » Ter Dez 30, 2014 11:24
por Hazengard » Ter Dez 30, 2014 11:24
Ei Molina, por favor, me tire uma dúvida!
Como você chegou no 16x?
Obrigado
-
Hazengard
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Dez 30, 2014 10:35
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Escola
- Andamento: cursando
 por juuheuh » Sáb Mai 21, 2016 13:11
por juuheuh » Sáb Mai 21, 2016 13:11
Apartir do momento em que é eliminado o 2 foi por conta de ter invertido a operação, assim ficaria
8x.2=16x
Espero ter ajudado.
-
juuheuh
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Mai 21, 2016 13:07
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Química
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Problema com triângulo incentro
 por Vinicius das duvidas » Ter Jul 14, 2015 21:57
por Vinicius das duvidas » Ter Jul 14, 2015 21:57
- 0 Respostas
- 2362 Exibições
- Última mensagem por Vinicius das duvidas

Ter Jul 14, 2015 21:57
Geometria Plana
-
- Incentro
 por Analt » Sex Mai 06, 2011 15:36
por Analt » Sex Mai 06, 2011 15:36
- 2 Respostas
- 3061 Exibições
- Última mensagem por Analt

Dom Mai 08, 2011 15:23
Geometria Plana
-
- incentro
por davipepe » Seg Ago 20, 2012 13:11
- 2 Respostas
- 1870 Exibições
- Última mensagem por davipepe

Seg Ago 20, 2012 23:53
Geometria Plana
-
- UFPB 2008 (Incentro)
por gomeslcs » Seg Set 13, 2010 15:14
- 3 Respostas
- 7542 Exibições
- Última mensagem por mcortes

Qua Abr 11, 2012 23:23
Geometria Plana
-
- Questão sobre triângulo incentro
 por LuizCarlos » Dom Abr 01, 2012 19:00
por LuizCarlos » Dom Abr 01, 2012 19:00
- 4 Respostas
- 7434 Exibições
- Última mensagem por LuizCarlos

Dom Abr 01, 2012 20:49
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



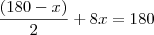
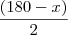 veio da soma da metade dos ângulos B e C, o
veio da soma da metade dos ângulos B e C, o 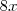 veio do ângulo BIC (enunciado) e 180 é a soma dos ângulos internos de um triângulo. Sendo assim:
veio do ângulo BIC (enunciado) e 180 é a soma dos ângulos internos de um triângulo. Sendo assim:





 (enunciado), o ângulo B mais o ângulo C vale
(enunciado), o ângulo B mais o ângulo C vale 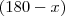 . Certo até aqui?
. Certo até aqui?



