 por Ramses » Qui Mar 31, 2016 17:31
por Ramses » Qui Mar 31, 2016 17:31
Dados os vetores
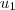
= (2,-1),
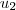
=(1,1)

= (-1,-1),
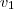
=(1,3),

=(2,3) e
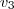
= (-5,-6). Decida se existe ou não um operador linear A:
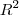
?
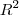
tal que

Eu fiz, mas não sei se tá certo, fiz assim
a*(2,-1) + b*(1,1) + c*(-1,-1) = (x,y)
Montei o sistema e encontrei b-c=

e a=
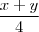
Depois fiz transformação
a*A

+ b-c*A
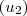
e obtive esse vetor w =
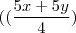
,
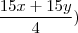
a minha dúvida é se meu raciocínio está correto e, se tiver, o que posso concluir disso? Eu acabei obtendo um r2 em r2, então quer dizer que é operador linear?
-
Ramses
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qui Mar 31, 2016 17:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Ciência da Computação
- Andamento: cursando
 por adauto martins » Sáb Abr 02, 2016 13:05
por adauto martins » Sáb Abr 02, 2016 13:05
uma matriz
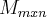
sempre determina uma transformaçao
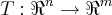
,assim como uma transformaçao linear T e determinada por uma matriz
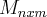
(prove isso)...
nesse nosso caso temos:
temos q. verificar se
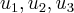
sao LI,e formam uma base p/
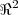
,assim como
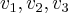
formam uma base p/
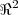
se assim proceder,poderemos ter:
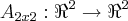
tal q. as sentenças sao verdadeiras...se caso positivo,encontre tal transformaçao...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvida: Transformações Lineares (Álgebra Linear)
por felipe_ad » Qua Out 13, 2010 16:00
- 2 Respostas
- 2558 Exibições
- Última mensagem por felipe_ad

Qua Out 20, 2010 10:27
Álgebra Linear
-
- [algebra linear]problema com transformações lineares
por clebrsonn » Qui Out 13, 2011 11:48
- 0 Respostas
- 1887 Exibições
- Última mensagem por clebrsonn

Qui Out 13, 2011 11:48
Álgebra Linear
-
- Álgebra Linear (Sistemas Lineares)
por AboraBR » Sex Ago 24, 2012 23:42
- 6 Respostas
- 3986 Exibições
- Última mensagem por AboraBR

Sáb Ago 25, 2012 21:01
Sistemas de Equações
-
- algebra linear e transfomações lineares
por bebelo32 » Ter Dez 09, 2014 01:02
- 1 Respostas
- 1773 Exibições
- Última mensagem por adauto martins

Ter Dez 09, 2014 14:44
Álgebra Linear
-
- algebra linear e transfomações lineares
por bebelo32 » Qua Jun 10, 2015 17:56
- 1 Respostas
- 9622 Exibições
- Última mensagem por DanielFerreira

Sáb Out 31, 2015 22:41
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
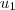 = (2,-1),
= (2,-1), 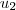 =(1,1)
=(1,1)  = (-1,-1),
= (-1,-1), 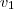 =(1,3),
=(1,3),  =(2,3) e
=(2,3) e 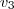 = (-5,-6). Decida se existe ou não um operador linear A:
= (-5,-6). Decida se existe ou não um operador linear A: 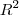 ?
?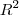 tal que
tal que 
 e a=
e a= 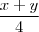
 + b-c*A
+ b-c*A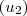
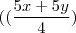 ,
, 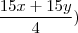


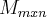 sempre determina uma transformaçao
sempre determina uma transformaçao 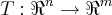 ,assim como uma transformaçao linear T e determinada por uma matriz
,assim como uma transformaçao linear T e determinada por uma matriz 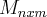 (prove isso)...
(prove isso)...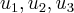 sao LI,e formam uma base p/
sao LI,e formam uma base p/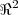 ,assim como
,assim como 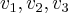 formam uma base p/
formam uma base p/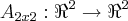 tal q. as sentenças sao verdadeiras...se caso positivo,encontre tal transformaçao...
tal q. as sentenças sao verdadeiras...se caso positivo,encontre tal transformaçao...
