 por Vilson » Ter Mar 08, 2016 21:18
por Vilson » Ter Mar 08, 2016 21:18
A forma do tanque deve ser na forma de um CILINDRO REGULAR COM UM HEMISFÉRIO EM CADA EXTREMIDADE. Se a capacidade desejada do tanque é de 5m³, quais as dimensões que exigem menor quantidade de aço ? Despreze a espessura das paredes?
-
Vilson
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Mar 08, 2016 21:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Fisica
- Andamento: cursando
 por adauto martins » Qui Mar 10, 2016 17:59
por adauto martins » Qui Mar 10, 2016 17:59
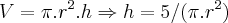
...
![{A}_{t}=2.\pi.{r}^{2}+2r.h=2\pi{r}^{2}+5/(\pi.r)\Rightarrow dA/dr=4.\pi.r-5.\pi/{r}^{2}\Rightarrow dA/dr=0\Rightarrow (4.\pi.{r}^{3}-5\pi)/{r}^{2}=0\Rightarrow 4.\pi.{r}^{3}-5\pi=0\Rightarrow 4.{r}^{3}-5=0\Rightarrow r=\sqrt[3]{(5/4)}...h=5/(\pi.\sqrt[3]{(25/16)} {A}_{t}=2.\pi.{r}^{2}+2r.h=2\pi{r}^{2}+5/(\pi.r)\Rightarrow dA/dr=4.\pi.r-5.\pi/{r}^{2}\Rightarrow dA/dr=0\Rightarrow (4.\pi.{r}^{3}-5\pi)/{r}^{2}=0\Rightarrow 4.\pi.{r}^{3}-5\pi=0\Rightarrow 4.{r}^{3}-5=0\Rightarrow r=\sqrt[3]{(5/4)}...h=5/(\pi.\sqrt[3]{(25/16)}](/latexrender/pictures/dfa1883c16d3e7ecc1bc3703c297bb04.png)
...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por rzarour » Dom Mar 13, 2016 01:17
por rzarour » Dom Mar 13, 2016 01:17
Preciso de uma luz para entender a resolução do problema proposto pelo Vilson, pois não consegui encontrar referência nos cálculos que considerassem "um hemisfério em cada extremidade", conforme enunciado da questão.
Grato!
-
rzarour
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Fev 29, 2016 02:05
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Técnico em Eletrotécnica
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Ajuda com calculo de derivada de função quociente
por alienpuke » Dom Out 25, 2015 15:31
- 1 Respostas
- 12556 Exibições
- Última mensagem por Cleyson007

Dom Out 25, 2015 16:47
Cálculo: Limites, Derivadas e Integrais
-
- [derivada] derivada pela definição da secante
por TheKyabu » Sáb Out 27, 2012 23:24
- 2 Respostas
- 10887 Exibições
- Última mensagem por TheKyabu

Dom Out 28, 2012 11:44
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Com duas variáveis e derivada mista
por leticiaeverson » Dom Abr 22, 2018 00:39
- 3 Respostas
- 13192 Exibições
- Última mensagem por Gebe

Dom Abr 22, 2018 17:11
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada]derivada de função de raiz cúbica
por armando » Sáb Jul 20, 2013 15:22
- 4 Respostas
- 14798 Exibições
- Última mensagem por armando

Dom Jul 21, 2013 22:17
Cálculo: Limites, Derivadas e Integrais
-
- [DERIVADA] DERIVADA POR DEFINIÇÃO DA RAIZ DO MÓDULO DE X
por Matheusgdp » Qua Set 16, 2015 04:07
- 2 Respostas
- 5115 Exibições
- Última mensagem por Matheusgdp

Qui Set 17, 2015 18:31
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



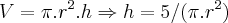 ...
...![{A}_{t}=2.\pi.{r}^{2}+2r.h=2\pi{r}^{2}+5/(\pi.r)\Rightarrow dA/dr=4.\pi.r-5.\pi/{r}^{2}\Rightarrow dA/dr=0\Rightarrow (4.\pi.{r}^{3}-5\pi)/{r}^{2}=0\Rightarrow 4.\pi.{r}^{3}-5\pi=0\Rightarrow 4.{r}^{3}-5=0\Rightarrow r=\sqrt[3]{(5/4)}...h=5/(\pi.\sqrt[3]{(25/16)} {A}_{t}=2.\pi.{r}^{2}+2r.h=2\pi{r}^{2}+5/(\pi.r)\Rightarrow dA/dr=4.\pi.r-5.\pi/{r}^{2}\Rightarrow dA/dr=0\Rightarrow (4.\pi.{r}^{3}-5\pi)/{r}^{2}=0\Rightarrow 4.\pi.{r}^{3}-5\pi=0\Rightarrow 4.{r}^{3}-5=0\Rightarrow r=\sqrt[3]{(5/4)}...h=5/(\pi.\sqrt[3]{(25/16)}](/latexrender/pictures/dfa1883c16d3e7ecc1bc3703c297bb04.png) ...
...

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.