Quanto à regra da cadeia, estou tendo dificuldade em relação às notações usadas. Ex.:
Se y = f(g(x)). A maioria dos livros e sites fazem:
u = g(x)
y = f(u)
E só então:
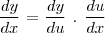
Não entendo por quê ou mesmo se isso é mesmo necessário. Pois u é uma função, mas g também já era uma função, então pra quê fazer u = g(x) e y = f(u) ? Eu não poderia simplesmente dizer que
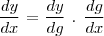?O que me leva a outra dúvida que não posso dissociar da dúvida exposta acima:
A regra da cadeia na notação de Lagrange seria:
[f(g(x))] ' = f ' (g(x)) . g ' (x)
Correto?
Pois bem, entendo que a derivada de y em relação a x (
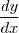) fornece a inclinação da reta tangente à curva y em um ponto de abscissa x e que, como y é uma função composta de f e g podemos obter essa derivada pela regra da cadeia. O que eu não entendo é o que significa o primeiro termo desse produto, o tal 
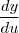. Seria a derivada de f em relação u? É a mesma coisa de f '(g(x)) na notação de Lagrange?
O que ele significa, o que ele fornece e como calculá-lo?
, avisa que eu resolvo.
