 por adlehs » Qui Nov 12, 2015 03:01
por adlehs » Qui Nov 12, 2015 03:01
Calcule o perímetro P e área S da seção produzida num octaedro regular circunscrito a uma esfera de
![\sqrt[]{6} \sqrt[]{6}](/latexrender/pictures/bd95d60cfbcfe62be13a43e39e60bbdb.png)
dm de diâmetro pelo plano que contém o centro dessa esfera e que é paralelo a umas das faces do octaedro.
Por favor, me ajudem! Não estou conseguindo imaginar como deve ser essa seção...
-
adlehs
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Nov 12, 2015 01:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
 por adauto martins » Sex Nov 13, 2015 16:13
por adauto martins » Sex Nov 13, 2015 16:13
como o poligono é rugilar seu angulo central sera
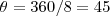
...o triangulo referente ao angulo central sera equilatero...logo...
seja l o lado do piligono,entao...
![{l}^{2}=2.{r}^{2}-2.{r}^{2}cos45=2.{r}^{2}(1-\sqrt[]{2}/2)=2.{(\sqrt[]{6}/2})^{2}.(1-\sqrt[]{2}/2) {l}^{2}=2.{r}^{2}-2.{r}^{2}cos45=2.{r}^{2}(1-\sqrt[]{2}/2)=2.{(\sqrt[]{6}/2})^{2}.(1-\sqrt[]{2}/2)](/latexrender/pictures/a15318a5f3236b598e3c4ce0d0f4755d.png)
![=2.(6/4).(1-\sqrt[]{2}/2)\Rightarrow l=\sqrt[]{3.(1-\sqrt[]{2}/2)} =2.(6/4).(1-\sqrt[]{2}/2)\Rightarrow l=\sqrt[]{3.(1-\sqrt[]{2}/2)}](/latexrender/pictures/a8ef2f87e2043dca0b51475646cebca2.png)
...lei dos cossenos...
![p=8.l...A=8.\sqrt[]{3}{l}^{2}/2=4.\sqrt[]{3}{l}^{2} p=8.l...A=8.\sqrt[]{3}{l}^{2}/2=4.\sqrt[]{3}{l}^{2}](/latexrender/pictures/033283aeb7a53491d12f0b2ad717576e.png)
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Sáb Nov 14, 2015 15:00
por adauto martins » Sáb Nov 14, 2015 15:00
correçao...
a soluçao apresentada anteriormente esta incorreta...
o triangulo nao é equilatero e sim isosceles...entao...
os angulos da base medem

...
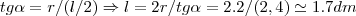
...
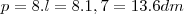
...
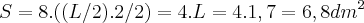
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Geometria Espacial
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Geometria Espacial] Octaedro regular
 por rochadapesada » Qui Abr 11, 2013 18:15
por rochadapesada » Qui Abr 11, 2013 18:15
- 2 Respostas
- 6288 Exibições
- Última mensagem por rochadapesada

Dom Abr 14, 2013 17:33
Geometria Espacial
-
- [Circunscrição de triângulos Retângulos]
 por Gustavo Gomes » Sáb Out 06, 2012 22:07
por Gustavo Gomes » Sáb Out 06, 2012 22:07
- 9 Respostas
- 4609 Exibições
- Última mensagem por jeanderson09

Qui Out 11, 2012 21:09
Geometria Plana
-
- O volume de uma esfera em relação a outra esfera
por Macedo Junior » Sáb Jul 23, 2016 21:01
- 2 Respostas
- 9582 Exibições
- Última mensagem por Macedo Junior

Sáb Jul 23, 2016 23:28
Geometria Plana
-
- [Poliedros] Cubo e Octaedro
 por andrecalegarif » Qui Nov 29, 2018 17:14
por andrecalegarif » Qui Nov 29, 2018 17:14
- 0 Respostas
- 5452 Exibições
- Última mensagem por andrecalegarif

Qui Nov 29, 2018 17:14
Geometria Plana
-
- Sólidos Geométricos
por Ismael_SAX » Seg Jan 09, 2012 02:13
- 1 Respostas
- 4014 Exibições
- Última mensagem por Molina

Qua Jan 11, 2012 13:17
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[]{6} \sqrt[]{6}](/latexrender/pictures/bd95d60cfbcfe62be13a43e39e60bbdb.png) dm de diâmetro pelo plano que contém o centro dessa esfera e que é paralelo a umas das faces do octaedro.
dm de diâmetro pelo plano que contém o centro dessa esfera e que é paralelo a umas das faces do octaedro.
![\sqrt[]{6} \sqrt[]{6}](/latexrender/pictures/bd95d60cfbcfe62be13a43e39e60bbdb.png) dm de diâmetro pelo plano que contém o centro dessa esfera e que é paralelo a umas das faces do octaedro.
dm de diâmetro pelo plano que contém o centro dessa esfera e que é paralelo a umas das faces do octaedro.
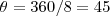 ...o triangulo referente ao angulo central sera equilatero...logo...
...o triangulo referente ao angulo central sera equilatero...logo...![{l}^{2}=2.{r}^{2}-2.{r}^{2}cos45=2.{r}^{2}(1-\sqrt[]{2}/2)=2.{(\sqrt[]{6}/2})^{2}.(1-\sqrt[]{2}/2) {l}^{2}=2.{r}^{2}-2.{r}^{2}cos45=2.{r}^{2}(1-\sqrt[]{2}/2)=2.{(\sqrt[]{6}/2})^{2}.(1-\sqrt[]{2}/2)](/latexrender/pictures/a15318a5f3236b598e3c4ce0d0f4755d.png)
![=2.(6/4).(1-\sqrt[]{2}/2)\Rightarrow l=\sqrt[]{3.(1-\sqrt[]{2}/2)} =2.(6/4).(1-\sqrt[]{2}/2)\Rightarrow l=\sqrt[]{3.(1-\sqrt[]{2}/2)}](/latexrender/pictures/a8ef2f87e2043dca0b51475646cebca2.png) ...lei dos cossenos...
...lei dos cossenos...![p=8.l...A=8.\sqrt[]{3}{l}^{2}/2=4.\sqrt[]{3}{l}^{2} p=8.l...A=8.\sqrt[]{3}{l}^{2}/2=4.\sqrt[]{3}{l}^{2}](/latexrender/pictures/033283aeb7a53491d12f0b2ad717576e.png)

 ...
...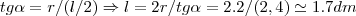 ...
...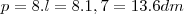 ...
...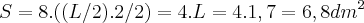


 .
.



