Estou com algumas dificuldades nos exercícios sobre matrizes, se alguém puder ajudar fico grata.
Na questão a seguir tenho que descobrir o valor de x, y, z , t.
Sabendo que A=(aij), tal que aij=i+j
|x+y x+z|
|3x-t t+z|
Bom nessa questão eu consegui calcular a11=2 a12=3 a21=3 a22=4, coloquei cada valor com seu respectvo corespondente mas não sei como calcular dois termos em uma só conta.
-------------------------------------------------------------------------------------------------------
Bom na matriz seguinte eu não sei qual dos valores coloco na letra correspondende, se tenho que fazer outra matriz ou se tenho que fazer algum outro calculo.
![C={\left[\frac{1}{4}B - \frac{1}{2}A \right]}^{t} C={\left[\frac{1}{4}B - \frac{1}{2}A \right]}^{t}](/latexrender/pictures/3bb2f60b7720844213949cbeec060db9.png) onde A=(2 -4 6) e B=(4 -8 12)
onde A=(2 -4 6) e B=(4 -8 12)----------------------------------------------------------------------------------------------------------
E nessa última eu queria saber se multiplico a pela sua matriz, e o b pela sua respectiva, ou se primeiro calculo x e y e como a resolvo.São essas as minha dúvidas, qualquer ajuda é bem vinda.Se alguém souber mais ou menos qual o caminho sigo para resolvelas ficarei muita grata
[
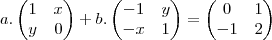


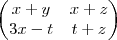
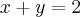
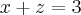
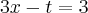
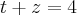



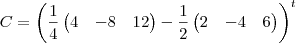
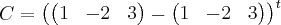
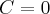
 e
e  e montar os sistemas, chegará nisso:
e montar os sistemas, chegará nisso: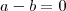
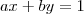
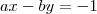

 pela primeira equação, e
pela primeira equação, e 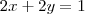
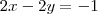
 . Assim, fica claro que
. Assim, fica claro que 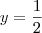 .
.


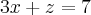 --> Primeira equação encontrada
--> Primeira equação encontrada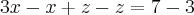

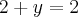

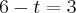

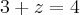
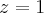

 .
.



