Vocë não nos disse o que já tentou fazer para resolver o problema. Favor ver as regras deste site. No entanto, vou responder esta sua pergunta, mas na próxima vez, para não ficar sem resposta, por favor, diga-nos tudo o que já tentou fazer para resolver seu problema e quais foram as reais dúvidas que apareceram para que nós não sejamos meros resolvedores de problema. Grato!
viewtopic.php?f=0&t=7543RESOLUÇÃO:
Em todos os casos, vamos chamar de S o valor do salário, S(x) a função que queremos e x, o valor da comissão. Desta maneira:
a) Escreva as leis de formação das funções envolvidas correspondentes ao salário recebido em cada uma das lojas pelo total de vendas.
Para a Loja A:
![{S}_{A}(x) = 750,00 + 0,02x \;\;\;\;\;\;[1] {S}_{A}(x) = 750,00 + 0,02x \;\;\;\;\;\;[1]](/latexrender/pictures/de06fb7e8523d99e6fb423c659676469.png)
Para a Loja B:
![{S}_{B}(x) = 0,05x \;\;\;\;\;\;\;\;[2] {S}_{B}(x) = 0,05x \;\;\;\;\;\;\;\;[2]](/latexrender/pictures/56f0fd40b60dd43eac69ceb3230fc473.png)
b) A partir de que valor mensal de vendas é mais vantajoso trabalhar na loja B?
Para sabermos disso, precisamos primeiramente saber em que ponto as vendas se igualam, ou seja, quando:
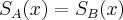
Assim:
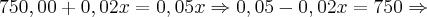
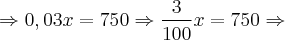
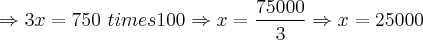
Assim, os dois salários serão iguais quando as vendas atingirem R$ 25.000,00! - Aumentando-se 1 real em x, poderemos então saber quem tem mais vantagem, ou seja, se é o Salário da Empresa A ou o Salário da Empresa B. Assim, vamos substituir o valor de x nas equações [1] e [2] por 25001 reais para sabermos qual é o mais vantajoso:
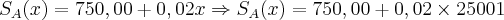
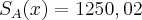
e por fim:
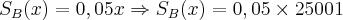
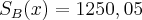
Portanto, o salário na Empresa B só será mais vantajoso que o Salário na Empresa A quando as vendas ultrapassarem R$ 25.000,00!

Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali


![{S}_{A}(x) = 750,00 + 0,02x \;\;\;\;\;\;[1] {S}_{A}(x) = 750,00 + 0,02x \;\;\;\;\;\;[1]](/latexrender/pictures/de06fb7e8523d99e6fb423c659676469.png)
![{S}_{B}(x) = 0,05x \;\;\;\;\;\;\;\;[2] {S}_{B}(x) = 0,05x \;\;\;\;\;\;\;\;[2]](/latexrender/pictures/56f0fd40b60dd43eac69ceb3230fc473.png)
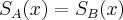
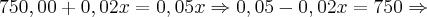
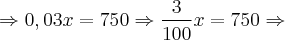
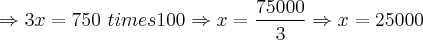
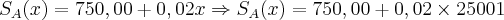
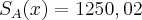
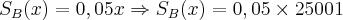
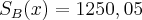




 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.