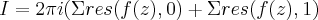por Russman » Ter Out 16, 2012 21:04
por Russman » Ter Out 16, 2012 21:04
Não estou conseguindo calcular o Resíduo da seguinte integral:
![I=\oint \frac{dz}{\sqrt[3]{z^2-z^3}} I=\oint \frac{dz}{\sqrt[3]{z^2-z^3}}](/latexrender/pictures/0d650773528e5a95a524874a9a10bac9.png)
.
Eu sei que o resultado será algo do tipo
![I=\oint \frac{dz}{\sqrt[3]{z^2-z^3}} = 2\pi i[b_1(z=0)+b_2(z=1)] I=\oint \frac{dz}{\sqrt[3]{z^2-z^3}} = 2\pi i[b_1(z=0)+b_2(z=1)]](/latexrender/pictures/ee5726d770436bb669f5bdbdcc3b93c1.png)
mas não consigo calcular os resíduos em

e em
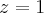
.
Alguém tem alguma sugestão?
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por adauto martins » Dom Out 11, 2015 15:15
por adauto martins » Dom Out 11, 2015 15:15
![f(z)=1/(\sqrt[3]{{z}^{2}(1-z)} f(z)=1/(\sqrt[3]{{z}^{2}(1-z)}](/latexrender/pictures/bcd639ea63dafa93afac0b1aebbf3f76.png)
...
faz-se
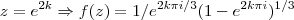
...
os polos serao de grau {3,6,9,...3p,...}...logo os residuos serao:
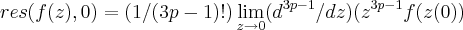
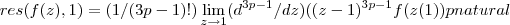
...
como nao se definiu a regiao de integraçao...
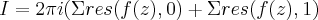
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Números Complexos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Teorema do Residuo de Cauchy]
por Gebe » Qua Jun 03, 2015 23:27
- 2 Respostas
- 3398 Exibições
- Última mensagem por adauto martins

Qua Mar 02, 2016 11:36
Cálculo: Limites, Derivadas e Integrais
-
- [Calculo]Alguém me ajuda nessa questão de calculo pfv.
por moeni » Seg Abr 04, 2022 21:54
- 0 Respostas
- 6491 Exibições
- Última mensagem por moeni

Seg Abr 04, 2022 21:54
Cálculo: Limites, Derivadas e Integrais
-
- [calculo] calculo de integral - coordenada esferica
por fatalshootxd » Ter Mar 31, 2015 00:43
- 1 Respostas
- 4532 Exibições
- Última mensagem por adauto martins

Sáb Abr 04, 2015 16:13
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo] Cálculo Polinômio Interpolador
 por barbara-rabello » Qui Out 22, 2015 20:07
por barbara-rabello » Qui Out 22, 2015 20:07
- 1 Respostas
- 2658 Exibições
- Última mensagem por adauto martins

Sáb Out 24, 2015 11:00
Cálculo: Limites, Derivadas e Integrais
-
- [Calculo] Exercícios de Calculo
por Thomas » Seg Mai 16, 2016 16:39
- 0 Respostas
- 0 Exibições
- Última mensagem por Visitante

Qua Dez 31, 1969 22:00
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![I=\oint \frac{dz}{\sqrt[3]{z^2-z^3}} I=\oint \frac{dz}{\sqrt[3]{z^2-z^3}}](/latexrender/pictures/0d650773528e5a95a524874a9a10bac9.png) .
.![I=\oint \frac{dz}{\sqrt[3]{z^2-z^3}} = 2\pi i[b_1(z=0)+b_2(z=1)] I=\oint \frac{dz}{\sqrt[3]{z^2-z^3}} = 2\pi i[b_1(z=0)+b_2(z=1)]](/latexrender/pictures/ee5726d770436bb669f5bdbdcc3b93c1.png)
 e em
e em 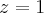 .
.
![I=\oint \frac{dz}{\sqrt[3]{z^2-z^3}} I=\oint \frac{dz}{\sqrt[3]{z^2-z^3}}](/latexrender/pictures/0d650773528e5a95a524874a9a10bac9.png) .
.![I=\oint \frac{dz}{\sqrt[3]{z^2-z^3}} = 2\pi i[b_1(z=0)+b_2(z=1)] I=\oint \frac{dz}{\sqrt[3]{z^2-z^3}} = 2\pi i[b_1(z=0)+b_2(z=1)]](/latexrender/pictures/ee5726d770436bb669f5bdbdcc3b93c1.png)
 e em
e em 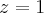 .
.
![f(z)=1/(\sqrt[3]{{z}^{2}(1-z)} f(z)=1/(\sqrt[3]{{z}^{2}(1-z)}](/latexrender/pictures/bcd639ea63dafa93afac0b1aebbf3f76.png) ...
...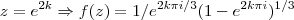 ...
...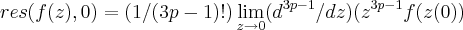
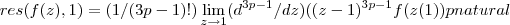 ...
...