 por misaelbarreto » Qua Set 16, 2015 18:05
por misaelbarreto » Qua Set 16, 2015 18:05
Estou com uma dúvida, na equação x = 9b - 36 sobre 9, porquê não posso cortar o 9 do numerador com o 9 do denominador?
-
misaelbarreto
-
 por nakagumahissao » Sex Set 18, 2015 15:23
por nakagumahissao » Sex Set 18, 2015 15:23
Misael,
Na realidade, o termo correto não seria cortar e sim, dividir cada membro do numerador pelo denominador. no caso específico que enviou, temos:
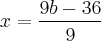
Note que esta divisão é o mesmo que dizermos:
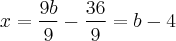
Vamos tomar um exemplo numérico para ficar mais claro:
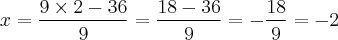
Que teria resultado semelhante fazendo-se da seguinte forma:
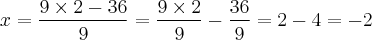
Preste bem atenção que dividimos cada membro da soma/subtração do numerador por um numerador que divida cada membro do numerador exatamente. Isto abaixo não pode ocorrer então:
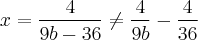
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por misaelbarreto » Sáb Set 19, 2015 18:03
por misaelbarreto » Sáb Set 19, 2015 18:03
Sim, dividir. Estou acostumado com a expressão "cortar". Não me recordava dessa propriedade das frações, obrigado pela informação.
-
misaelbarreto
-
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação com Frações
por carolvbuenos » Qui Dez 30, 2010 20:18
- 1 Respostas
- 3130 Exibições
- Última mensagem por MarceloFantini

Qui Dez 30, 2010 20:35
Sistemas de Equações
-
- simplificação da equação
por Bella » Sex Jun 10, 2011 12:54
- 1 Respostas
- 1525 Exibições
- Última mensagem por deangelo

Sex Jun 10, 2011 16:00
Trigonometria
-
- Simplificação de equação
por Laio » Sáb Fev 15, 2014 20:12
- 2 Respostas
- 3413 Exibições
- Última mensagem por Laio

Ter Fev 25, 2014 22:00
Equações
-
- Simplificação de Equação
por adna » Qua Mar 26, 2014 15:48
- 0 Respostas
- 857 Exibições
- Última mensagem por adna

Qua Mar 26, 2014 15:48
Equações
-
- Equação com frações e parenteses
por LeonardoOZ » Sáb Jan 26, 2013 20:01
- 3 Respostas
- 4729 Exibições
- Última mensagem por DanielFerreira

Qui Jan 31, 2013 22:44
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


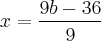
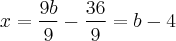
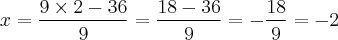
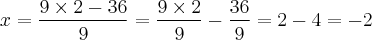
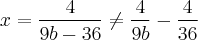



 , avisa que eu resolvo.
, avisa que eu resolvo.

