 por Crisaluno » Qui Set 03, 2015 04:37
por Crisaluno » Qui Set 03, 2015 04:37
Estou com uma dúvida nessas 3 questões:
1°) Sejam f um escalar e F um campo vetorial quaisquer. Se existem as derivadas parciais provar: div(f F) = f [ div(F)] + [ grad(f)] * F
2°)Se r(vetor)= xi + yj + zk é o chamado vetor posição, provar:
a) div(r) = 3
b) rot(r) = 0
c)Nabla II r II = r / |r|
3°) define-se nabla^2 como operador Laplaciano.
a) definir nabla^2 através de derivadas parciais;
b) se f e g são funções escalares dotadas de derivadas parciais segundas, provar :
nabla*(nabla f )= nabla^2 f
Segue o gabarito com as respostas :
1°)div (F) = f [div (F)] + [ grad (f) ] * F...é verdadeira.
2°) a) div (r) =3 ; b) rot (r) = 0 ; c) Nabla |r|= r / |r|...verdadeira
3°)verdadeira..
obs: Estou tendo muita dificuldade de com esses exercícios. seria possível mostrar o passo a passo até o resultado?
-
Crisaluno
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Set 03, 2015 03:38
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
 por adauto martins » Sáb Set 05, 2015 12:28
por adauto martins » Sáb Set 05, 2015 12:28
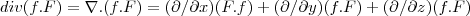
..MEU EDITOR NAO ESTA FUNCIONANDO AQUI,MAS VAMOS LA NO JEITO Q. DER...
a)
div(f.F)=(D/x)(f.F)+(D/y)(f.F)+(D/z)(f.F),onde (D/x),(D/y),(D/z) sao as derivadas parciais em relaçao aos eixos x,y,z...
div(f.F)=(Df(x).F+DF(x).f)+(Df(y).F+DF(y).f)+(D(z)f+D(F(z))=f.(DF(x)+DF(y)+DF(z))+(Df(x)+Df(y)+Df(z))=f.div(F)+grad(f).F,aqui usei a regra da derivada do produto...
b)
r=(x,y,z)...div(r)=(D/x)r+(D/y)r+(D/z)=1+1+1=3
c)
rot(r)=produto vetrorial de r...olha sem o editor,te fala nuum da...espero q. entensa ai o q. fiz...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por Crisaluno » Dom Set 06, 2015 02:08
por Crisaluno » Dom Set 06, 2015 02:08
Muito obrigado!!!Muito obrigado mesmo...conseg ui acompanhar sua resolução.
-
Crisaluno
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Set 03, 2015 03:38
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Rotacional e Divergente
por thiagodr » Sáb Abr 07, 2012 02:34
- 2 Respostas
- 1763 Exibições
- Última mensagem por thiagodr

Sáb Abr 07, 2012 16:27
Cálculo: Limites, Derivadas e Integrais
-
- Cálculo divergente e rotacional
 por Fernandobertolaccini » Qui Jun 11, 2015 20:23
por Fernandobertolaccini » Qui Jun 11, 2015 20:23
- 1 Respostas
- 1321 Exibições
- Última mensagem por adauto martins

Qua Jun 17, 2015 17:35
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Rotacional
por carvalhothg » Seg Mar 26, 2012 08:54
- 3 Respostas
- 2211 Exibições
- Última mensagem por LuizAquino

Ter Mar 27, 2012 12:51
Cálculo: Limites, Derivadas e Integrais
-
- Dúvida em Rotacional
por Lucasoaresf » Sáb Set 13, 2014 16:01
- 0 Respostas
- 963 Exibições
- Última mensagem por Lucasoaresf

Sáb Set 13, 2014 16:01
Cálculo: Limites, Derivadas e Integrais
-
- Dirvergência e rotacional de vetores unitários
por Jhenrique » Sáb Fev 01, 2014 09:54
- 0 Respostas
- 993 Exibições
- Última mensagem por Jhenrique

Sáb Fev 01, 2014 09:54
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


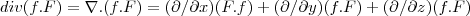 ..MEU EDITOR NAO ESTA FUNCIONANDO AQUI,MAS VAMOS LA NO JEITO Q. DER...
..MEU EDITOR NAO ESTA FUNCIONANDO AQUI,MAS VAMOS LA NO JEITO Q. DER...


 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.