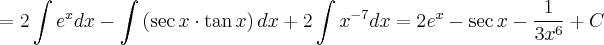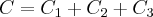por leticiapires52 » Qua Ago 12, 2015 16:37
por leticiapires52 » Qua Ago 12, 2015 16:37
1- Com o auxílio da tebela de integrais imedistas, determine a integral, a seguir:
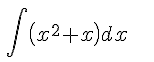
- questao 1.png (1.05 KiB) Exibido 1983 vezes
2- Utilizando a tabela de integração imediata, o cálculo para a expressão
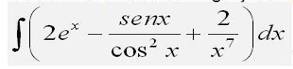
- questao 2.png (16.03 KiB) Exibido 1983 vezes
, resulta exatamente:
OBS: Se alguém souber algum site que posso achar a tabela de integrais imediatas.
-
leticiapires52
- Colaborador Voluntário

-
- Mensagens: 100
- Registrado em: Qua Fev 12, 2014 10:12
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por nakagumahissao » Qui Ago 13, 2015 11:43
por nakagumahissao » Qui Ago 13, 2015 11:43
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por leticiapires52 » Qui Ago 13, 2015 13:47
por leticiapires52 » Qui Ago 13, 2015 13:47
Muito obrigado
-
leticiapires52
- Colaborador Voluntário

-
- Mensagens: 100
- Registrado em: Qua Fev 12, 2014 10:12
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [integrais] Calculando áreas - Integrais
 por Faby » Seg Set 19, 2011 10:55
por Faby » Seg Set 19, 2011 10:55
- 11 Respostas
- 8866 Exibições
- Última mensagem por LuizAquino

Qua Set 21, 2011 18:03
Cálculo: Limites, Derivadas e Integrais
-
- Integrais
por pseytow » Qui Nov 27, 2008 21:54
- 1 Respostas
- 2818 Exibições
- Última mensagem por Adriano Tavares

Qui Mar 10, 2011 01:52
Cálculo: Limites, Derivadas e Integrais
-
- Integrais
por panneitz » Dom Jun 07, 2009 19:55
- 1 Respostas
- 2445 Exibições
- Última mensagem por Marcampucio

Dom Jun 07, 2009 20:31
Cálculo: Limites, Derivadas e Integrais
-
- Integrais
por leha » Ter Nov 10, 2009 16:08
- 2 Respostas
- 2534 Exibições
- Última mensagem por leha

Sex Nov 13, 2009 08:56
Cálculo: Limites, Derivadas e Integrais
-
- Integrais em IR3
por Saruman » Sáb Mai 22, 2010 10:27
- 1 Respostas
- 2141 Exibições
- Última mensagem por luispereira

Ter Dez 28, 2010 01:45
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


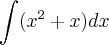
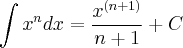
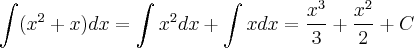
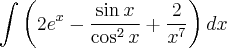
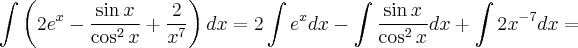
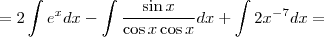
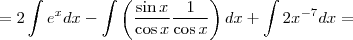
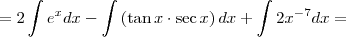
![= 2\int e^x dx -\int \left(\sec x \cdot \tan x \right) dx + 2\int x^{-7} dx \;\;\; [1] = 2\int e^x dx -\int \left(\sec x \cdot \tan x \right) dx + 2\int x^{-7} dx \;\;\; [1]](/latexrender/pictures/94bce72bbe1a2e46b413167c1e981290.png)
![\int e^{u} du = e^u + C \;\;\; [2] \int e^{u} du = e^u + C \;\;\; [2]](/latexrender/pictures/6ce11cd3eff73e310096795a5c15a5d0.png)
![\int (\sec u \tan u) dx = \sec u + C \;\;\; [3] \int (\sec u \tan u) dx = \sec u + C \;\;\; [3]](/latexrender/pictures/7655028a94ce463bba2dd6c871a4dce7.png)
![\int x^n dx = \frac{x^{(n+1)}}{n+1} + C \;\;\; [4] \int x^n dx = \frac{x^{(n+1)}}{n+1} + C \;\;\; [4]](/latexrender/pictures/d652b63db9046e6fe3de2671c6a23eec.png)
![2\int e^x dx = 2 \cdot(e^x) + {C}_{1} \;\;\;\;\; [5] 2\int e^x dx = 2 \cdot(e^x) + {C}_{1} \;\;\;\;\; [5]](/latexrender/pictures/39e4a420a000fda9236fbcabba6400cc.png)
![\int \left(\sec x \cdot \tan x \right) dx = \sec x + {C}_{2} \;\;\;\;\; [6] \int \left(\sec x \cdot \tan x \right) dx = \sec x + {C}_{2} \;\;\;\;\; [6]](/latexrender/pictures/3165f7886af07f0dc8f11c2a204b6b17.png)
![2\int x^{-7} dx = 2 \cdot \left(\frac{{x}^{-7 + 1}}{-7+1} \right) + {C}_{3} = 2 \cdot \left(\frac{{x}^{-6}}{-6} \right) + {C}_{3} = -\frac{1}{3{x}^{6}} + {C}_{3} \;\;\;\;\; [7] 2\int x^{-7} dx = 2 \cdot \left(\frac{{x}^{-7 + 1}}{-7+1} \right) + {C}_{3} = 2 \cdot \left(\frac{{x}^{-6}}{-6} \right) + {C}_{3} = -\frac{1}{3{x}^{6}} + {C}_{3} \;\;\;\;\; [7]](/latexrender/pictures/0a7ddaa798f7ba9bb7b714f5d47366a3.png)