 por zenildo » Qua Jul 15, 2015 11:13
por zenildo » Qua Jul 15, 2015 11:13
1) O lado, o perímetro e a área de um triângulo equilátero, nesta ordem, são termos de uma Progressão Geométrica. Assim, a medida da altura desse triângulo equilátero é em unidades de comprimento:
a) 12 raiz quadrada de 3
b) 6 raiz quadrada de 3
c) 3
d) 18
-
zenildo
- Colaborador Voluntário

-
- Mensagens: 309
- Registrado em: Sáb Abr 06, 2013 20:12
- Localização: SALVADOR-BA, TERRA DO AXÉ! BAÊA!!!!!
- Formação Escolar: EJA
- Área/Curso: PRETENDO/ DIREITO
- Andamento: cursando
 por nakagumahissao » Qua Jul 15, 2015 12:09
por nakagumahissao » Qua Jul 15, 2015 12:09
Zenildo,
O que já tentou fazer? O que não está entendendo? Qual é sua dúvida? -
viewtopic.php?f=0&t=7543A resposta é a letra (a), porém, creio que o pessoal aqui não irão te responder facilmente porque o objetivo aqui é que as dúvidas sejam sanadas e a pessoa que postou tenha aprendido um pouco mais que antes para que não seja apenas mais um site para se obter problemas resolvidos e os instrutores não passem somente por pessoas que resolvam exercícios e trabalhos dos outros, se é que me entende. Portanto, se puder, por favor exponha suas dúvidas e nos diga aonde ou o que não está entendo para que as pessoas deste fórum possam te ajudar a aprender ou entender mais sobre a matemática.
Deixei o link das regras de postagem deste fórum no link acima caso não tenha visto ainda.
Grato
Sandro
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por zenildo » Qua Jul 15, 2015 19:19
por zenildo » Qua Jul 15, 2015 19:19
como é que eu faço essa questão porque ela pede progressão geométrica. Faça o seguinte: demonstre ela algebricamente.
-
zenildo
- Colaborador Voluntário

-
- Mensagens: 309
- Registrado em: Sáb Abr 06, 2013 20:12
- Localização: SALVADOR-BA, TERRA DO AXÉ! BAÊA!!!!!
- Formação Escolar: EJA
- Área/Curso: PRETENDO/ DIREITO
- Andamento: cursando
 por zenildo » Qua Jul 15, 2015 19:38
por zenildo » Qua Jul 15, 2015 19:38
Primeiramente: sei que a altura é h= (l?3)/2; a área: A=(l²?3)/4 e o lado é l.
-
zenildo
- Colaborador Voluntário

-
- Mensagens: 309
- Registrado em: Sáb Abr 06, 2013 20:12
- Localização: SALVADOR-BA, TERRA DO AXÉ! BAÊA!!!!!
- Formação Escolar: EJA
- Área/Curso: PRETENDO/ DIREITO
- Andamento: cursando
 por nakagumahissao » Qui Jul 16, 2015 03:34
por nakagumahissao » Qui Jul 16, 2015 03:34
A progressão geométrica consiste em encontrarmos o lado 'x' fo triângulo equilátero, seu perímetro 3x e a área do mesmo.
Vamos calcular a altura deste triângulo de três lados iguais, de base b = x e hipotenusa x. Usando Pitágoras, tem-se que:
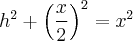
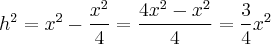
![h = \sqrt[]{\frac{3}{4}x^2} \Leftrightarrow h = \frac{x \cdot \sqrt[]{3}}{2} h = \sqrt[]{\frac{3}{4}x^2} \Leftrightarrow h = \frac{x \cdot \sqrt[]{3}}{2}](/latexrender/pictures/fe40ecaac1b798d4c5baa0bea0fb5f56.png)
A área deste triângulo será;
![A = \frac{bh}{2} = \frac{x}{2}\frac{x \cdot \sqrt[]{3}}{2} = \frac{x^2 \cdot \sqrt[]{3}}{4} A = \frac{bh}{2} = \frac{x}{2}\frac{x \cdot \sqrt[]{3}}{2} = \frac{x^2 \cdot \sqrt[]{3}}{4}](/latexrender/pictures/4e47c625296e653b92f2f10a9358925d.png)
Então, nossa sequência será:
![\left(x, 3x, \frac{x^2 \cdot \sqrt[]{3}}{4} \right ) \left(x, 3x, \frac{x^2 \cdot \sqrt[]{3}}{4} \right )](/latexrender/pictures/f7198fa8e453700ff7a859cad6cf1ef6.png)
A razão desta PG é obtida dividindo-se o valor subsequente pelo seu antecessor, assim:
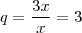
![q = \frac {\frac{x^2 \cdot \sqrt[]{3}}{4}}{3x} = \frac{x^2 \cdot \sqrt[]{3}}{3x \times 4} =\frac{x \cdot \sqrt[]{3}}{12} q = \frac {\frac{x^2 \cdot \sqrt[]{3}}{4}}{3x} = \frac{x^2 \cdot \sqrt[]{3}}{3x \times 4} =\frac{x \cdot \sqrt[]{3}}{12}](/latexrender/pictures/19df440a9936fcd0910d1cfb8cadf6c1.png)
7
Dos dois resultados acima, sabemos que as duas razões obtidas deverão ser iguais. Assim,
![\frac{x \cdot \sqrt[]{3}}{12} = 3 \Rightarrow x = \frac{3 \times 12}{\sqrt[]{3}} \Leftrightarrow x = \frac{36}{\sqrt[]{3}} \frac{x \cdot \sqrt[]{3}}{12} = 3 \Rightarrow x = \frac{3 \times 12}{\sqrt[]{3}} \Leftrightarrow x = \frac{36}{\sqrt[]{3}}](/latexrender/pictures/357097312c887481a05999c6ddbee626.png)
Racionalizando, ou seja, multiplicando-se o numerador e o denominador por raiz de três, teremos:
![x = \frac{36\sqrt[]{3}}{\sqrt[]{3} \times \sqrt[]{3}} \Leftrightarrow x = \frac{36 \sqrt[]{3}}{3} \Leftrightarrow x = 12\sqrt[]{3} x = \frac{36\sqrt[]{3}}{\sqrt[]{3} \times \sqrt[]{3}} \Leftrightarrow x = \frac{36 \sqrt[]{3}}{3} \Leftrightarrow x = 12\sqrt[]{3}](/latexrender/pictures/918f8a846b4fb6becd4b060da790c9b0.png)
Por fim, nossa PG terá a seguinte sequência:
![\left(12\sqrt[]{3}, \, 36\sqrt[]{3}, \, 108\sqrt[]{3}\right) \left(12\sqrt[]{3}, \, 36\sqrt[]{3}, \, 108\sqrt[]{3}\right)](/latexrender/pictures/748cee0e8a67f449bf23beb55b639787.png)
E portanto, a resposta é a letra (a)!

Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Triângulo Equilatéro
por Cleyson007 » Seg Mai 25, 2009 08:15
- 6 Respostas
- 3147 Exibições
- Última mensagem por ginrj

Dom Jun 07, 2009 20:39
Geometria Plana
-
- Triangulo Equilatero e GA
por isabelamiaki » Seg Abr 05, 2010 13:19
- 1 Respostas
- 2773 Exibições
- Última mensagem por Elcioschin

Seg Abr 05, 2010 22:09
Geometria Analítica
-
- [Triangulo equilátero]
por Andreza » Dom Out 23, 2011 11:42
- 2 Respostas
- 1581 Exibições
- Última mensagem por Andreza

Sáb Nov 12, 2011 09:56
Geometria Plana
-
- Triângulo Equilátero
 por Pri Ferreira » Qua Mar 21, 2012 14:30
por Pri Ferreira » Qua Mar 21, 2012 14:30
- 1 Respostas
- 1806 Exibições
- Última mensagem por LuizAquino

Sáb Mar 31, 2012 13:56
Geometria Plana
-
- Triângulo equilátero ( urgente)
 por Carlos28 » Seg Mar 17, 2014 12:36
por Carlos28 » Seg Mar 17, 2014 12:36
- 2 Respostas
- 1754 Exibições
- Última mensagem por Carlos28

Ter Mar 18, 2014 15:24
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


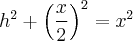
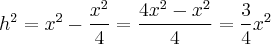
![h = \sqrt[]{\frac{3}{4}x^2} \Leftrightarrow h = \frac{x \cdot \sqrt[]{3}}{2} h = \sqrt[]{\frac{3}{4}x^2} \Leftrightarrow h = \frac{x \cdot \sqrt[]{3}}{2}](/latexrender/pictures/fe40ecaac1b798d4c5baa0bea0fb5f56.png)
![A = \frac{bh}{2} = \frac{x}{2}\frac{x \cdot \sqrt[]{3}}{2} = \frac{x^2 \cdot \sqrt[]{3}}{4} A = \frac{bh}{2} = \frac{x}{2}\frac{x \cdot \sqrt[]{3}}{2} = \frac{x^2 \cdot \sqrt[]{3}}{4}](/latexrender/pictures/4e47c625296e653b92f2f10a9358925d.png)
![\left(x, 3x, \frac{x^2 \cdot \sqrt[]{3}}{4} \right ) \left(x, 3x, \frac{x^2 \cdot \sqrt[]{3}}{4} \right )](/latexrender/pictures/f7198fa8e453700ff7a859cad6cf1ef6.png)
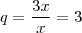
![q = \frac {\frac{x^2 \cdot \sqrt[]{3}}{4}}{3x} = \frac{x^2 \cdot \sqrt[]{3}}{3x \times 4} =\frac{x \cdot \sqrt[]{3}}{12} q = \frac {\frac{x^2 \cdot \sqrt[]{3}}{4}}{3x} = \frac{x^2 \cdot \sqrt[]{3}}{3x \times 4} =\frac{x \cdot \sqrt[]{3}}{12}](/latexrender/pictures/19df440a9936fcd0910d1cfb8cadf6c1.png) 7
7![\frac{x \cdot \sqrt[]{3}}{12} = 3 \Rightarrow x = \frac{3 \times 12}{\sqrt[]{3}} \Leftrightarrow x = \frac{36}{\sqrt[]{3}} \frac{x \cdot \sqrt[]{3}}{12} = 3 \Rightarrow x = \frac{3 \times 12}{\sqrt[]{3}} \Leftrightarrow x = \frac{36}{\sqrt[]{3}}](/latexrender/pictures/357097312c887481a05999c6ddbee626.png)
![x = \frac{36\sqrt[]{3}}{\sqrt[]{3} \times \sqrt[]{3}} \Leftrightarrow x = \frac{36 \sqrt[]{3}}{3} \Leftrightarrow x = 12\sqrt[]{3} x = \frac{36\sqrt[]{3}}{\sqrt[]{3} \times \sqrt[]{3}} \Leftrightarrow x = \frac{36 \sqrt[]{3}}{3} \Leftrightarrow x = 12\sqrt[]{3}](/latexrender/pictures/918f8a846b4fb6becd4b060da790c9b0.png)
![\left(12\sqrt[]{3}, \, 36\sqrt[]{3}, \, 108\sqrt[]{3}\right) \left(12\sqrt[]{3}, \, 36\sqrt[]{3}, \, 108\sqrt[]{3}\right)](/latexrender/pictures/748cee0e8a67f449bf23beb55b639787.png)






