1) Como o dinheiro está entre os atributos que se supõe trazer felicidade, uma grande parcela da população vê, nos jogos de loteria, a
esperança de realização de sonhos como ter carro, casa própria, fazer viagens, ajudar a família etc.
Com esse propósito, X costuma jogar na Mega Sena e usa diferentes critérios para a escolha dos números para cada aposta que faz.
Certo dia, enquanto estudava funções polinomiais, teve a ideia de fazer um jogo utilizando de P(x)=2x³-30x²+108x- 80.
a) as raízes
b) a soma dessas raízes
c) o produto dessas raízes
d) a soma do produtos dessas raízes consideradas duas a duas
Com base nessas informações determine os n° que X escolheu para fazer o referido jogo.


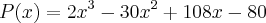
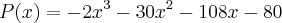
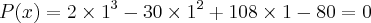
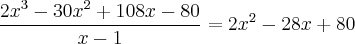
![\sqrt[]{\Delta} = \sqrt[]{b^2 - 4ac} = \sqrt[]{(-28)^2 - 4 (2)(80)} \sqrt[]{\Delta} = \sqrt[]{b^2 - 4ac} = \sqrt[]{(-28)^2 - 4 (2)(80)}](/latexrender/pictures/092944229ffda7b359cad10745945e68.png)
![\sqrt[]{\Delta} = \sqrt[]{144} = 12 \sqrt[]{\Delta} = \sqrt[]{144} = 12](/latexrender/pictures/85536704a5026b458ac3303f8c574d93.png)
![x = \frac{-b \pm \sqrt[]{\Delta}}{2a}=\frac{28 \pm 12}{4} x = \frac{-b \pm \sqrt[]{\Delta}}{2a}=\frac{28 \pm 12}{4}](/latexrender/pictures/f06316fbb69f204dff91f8308d1ab2a2.png)
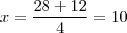
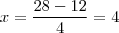

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
