Ta difícil essa analise

por **mat_MED** » Sáb Jun 06, 2015 11:09

Bom dia! Segue exercício:
Em uma estante há 6 livros de diferentes de matemática, 5 livros diferentes de física e 4 livros diferentes de química. Assinale a alternativa que indique de quantas maneiras diferentes é possível escolher 4 livros nessa estante de modo que haja pelo menos 1 livro de cada uma das três matérias.
a)240
b)300
c)540
d)720
e)800

por **DanielFerreira** » Dom Jun 07, 2015 10:33

TALVEZ, o gabarito esteja errado!!

Fiz assim:

M M F Q => um livro de cada disciplina MAIS um de matemática;

M F F Q => um livro de cada disciplina MAIS um de física;

M F Q Q => um livro de cada disciplina MAIS um de química;

M M M F => (...) faltou o de química; disso podemos concluir que não podemos ter três livros de uma disciplina. Com isso, vamos às contas!!

Encontremos a quantidade de escolhas possíveis no formato MMFQ:

- matemática => $C_{6, 2}$ ;
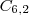
- física ======> $C_{5, 1}$ ;
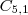
- química ====> $C_{4, 1}$ .

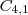
Daí, o total escolhas nesse formato é dado por: $C_{6, 2} \cdot C_{5, 1} \cdot C_{4, 1} = 300$

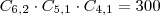
Encontremos a quantidade de escolhas possíveis no formato MFFQ:

- matemática => $C_{6, 1}$ ;
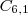
- física ======> $C_{5, 2}$ ;
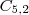
- química ====> $C_{4, 1}$ .

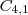
Daí, o total escolhas nesse formato é dado por: $C_{6, 1} \cdot C_{5, 2} \cdot C_{4, 1} = 240$

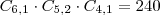
Tente concluir! para isso será necessário encontrar a quantidade de escolhas para o formato MFQQ, depois basta somá-lo aos valores encontrados (300 e 240).

A propósito, procure ser mais objetivo no título de post.
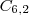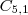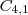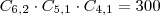
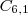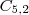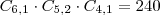