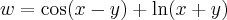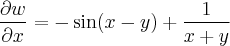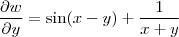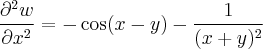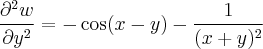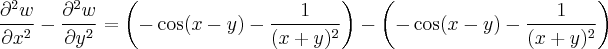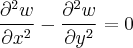Derivada como resolver

por **neoreload** » Dom Mai 10, 2015 07:36

Como resolver essa:

Se w = cos(x ? y) + ln(x + y) , mostre que: Imagem

Infelizmente não tenho a resposta dessa.

por **nakagumahissao** » Qua Out 07, 2015 09:53

De acordo com as regras do site, você deveria ter colocado junto com o enunciado, tudo o que já tinha tentado fazer para resolver o problema e postar também em que ponto a dúvida surgiu e que dúvida era. Creio que por causa disso, acabou ficando sem uma resposta para a sua postagem. Na próxima vez, por favor não se esqueça de seguir o regulamento para não acontecer isto novamente.

Resolvendo seu problema agora, se ainda estiver interessado.

RESOLUÇÃO:

Basta que utilizemos as derivadas parciais primeira e segunda sobre a equação dada e mostrar que a diferença entre eles dará zero.

Assim, tirando as derivadas parciais primeira de w tem-se que:

$w = \cos (x-y) + \ln (x + y)$

$\frac{\partial w}{\partial x} = -\sin (x - y) + \frac{1}{x + y}$

$\frac{\partial w}{\partial y} = \sin (x - y) + \frac{1}{x + y}$

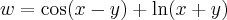
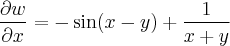
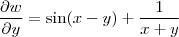
As segundas derivadas serão:

$\frac{\partial^{2} w}{\partial x^{2}} = -\cos (x-y) - \frac{1}{(x+y)^{2}}$

$\frac{\partial^{2} w}{\partial y^{2}} = -\cos (x-y) - \frac{1}{(x+y)^{2}}$

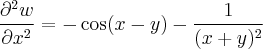
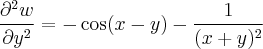
Assim, finalmente,

$\frac{\partial^{2} w}{\partial x^{2}} - \frac{\partial^{2} w}{\partial y^{2}} = \left(-\cos (x-y) - \frac{1}{(x+y)^{2}} \right) - \left(-\cos (x-y) - \frac{1}{(x+y)^{2}} \right)$

$\frac{\partial^{2} w}{\partial x^{2}} - \frac{\partial^{2} w}{\partial y^{2}} = 0$

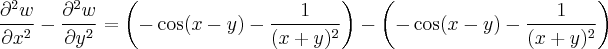
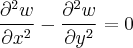
Como queríamos demonstrar. $\blacksquare$

Derivada como resolver

Derivada como resolver

Derivada como resolver

Re: Derivada como resolver

Quem está online