 por Pessoa Estranha » Dom Mai 03, 2015 23:55
por Pessoa Estranha » Dom Mai 03, 2015 23:55
Olá, preciso muito de ajuda para resolver a seguinte questão:
Calcule
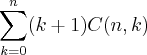
.
Muito Obrigada!
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por alexandre_de_melo » Qua Jul 29, 2015 22:46
por alexandre_de_melo » Qua Jul 29, 2015 22:46
-
alexandre_de_melo
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Ter Fev 25, 2014 12:00
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. em Matemática
- Andamento: formado
-
Voltar para Análise Combinatória
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- TRIANGULO DE PASCAL
por natanskt » Sex Dez 03, 2010 17:00
- 2 Respostas
- 2995 Exibições
- Última mensagem por natanskt

Seg Dez 06, 2010 10:43
Binômio de Newton
-
- [TRIANGULO DE PASCAL] URGENTE!
por Isa123 » Qui Jan 02, 2014 10:02
- 1 Respostas
- 1694 Exibições
- Última mensagem por Renato_RJ

Qui Jan 02, 2014 16:49
Análise Combinatória
-
- Discussão de uma questão do Triangulo de Pascal
por gustavoluiss » Sex Set 30, 2011 21:42
- 3 Respostas
- 3957 Exibições
- Última mensagem por gustavoluiss

Dom Out 02, 2011 19:06
Binômio de Newton
-
- Triangulo de Pascal e Trinômio de Newton
por Jhenrique » Sáb Nov 03, 2012 18:49
- 2 Respostas
- 4502 Exibições
- Última mensagem por Jhenrique

Sáb Nov 03, 2012 21:46
Binômio de Newton
-
- (( Analise combinatória ))
por Roberta » Dom Jul 13, 2008 17:28
- 8 Respostas
- 16378 Exibições
- Última mensagem por Aparecida

Sáb Mai 05, 2012 00:07
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
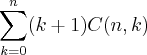 .
.
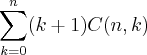 .
.
![\sum_{0}^{n}(k+1)\left(^n _k \right)= \sum_{0}^{n}(k+1)\frac{n!}{k!(n-k)!}=\sum_{0}^{n}[k\frac{n!}{k!(n-k)!}+\frac{n!}{k!(n-k)!}] \sum_{0}^{n}(k+1)\left(^n _k \right)= \sum_{0}^{n}(k+1)\frac{n!}{k!(n-k)!}=\sum_{0}^{n}[k\frac{n!}{k!(n-k)!}+\frac{n!}{k!(n-k)!}]](/latexrender/pictures/6e618652bd2c92f065ae7c94528829e6.png)
![=\sum_{1}^{n}[k\frac{n!}{k!(n-k)!}]+\sum_{0}^{n}[\frac{n!}{k!(n-k)!}] = \sum_{1}^{n}[\frac{n!}{(k-1)!(n-k)!}]+\sum_{0}^{n}[\frac{n!}{k!(n-k)!}] =\sum_{1}^{n}[k\frac{n!}{k!(n-k)!}]+\sum_{0}^{n}[\frac{n!}{k!(n-k)!}] = \sum_{1}^{n}[\frac{n!}{(k-1)!(n-k)!}]+\sum_{0}^{n}[\frac{n!}{k!(n-k)!}]](/latexrender/pictures/2ec015176100906bf68f417bcd74f1c1.png)
![=n\sum_{1}^{n}[\frac{(n-1)!}{(k-1)![(n-1)-(k-1)]!}]+\sum_{0}^{n}\left(^n _k \right) =n\sum_{1}^{n}[\frac{(n-1)!}{(k-1)![(n-1)-(k-1)]!}]+\sum_{0}^{n}\left(^n _k \right)](/latexrender/pictures/a8e69a16095c9f87f5d83efb190bbdac.png)
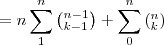

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.