Considere a função:
f (x) = x se x é racional, 1/x se x é irracional
Qual o maior elemento do conjunto?
{ f (7/31), f (1), f (3,14), f ( ? 24/? 2) }
Alguem saberia me explicar como se chega no resultado?



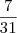 Racional
Racional Racional
Racional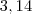 Racional. Lembrando que \pi é irracional, mas 3,14 é racional.
Racional. Lembrando que \pi é irracional, mas 3,14 é racional. 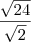 Irracional
Irracional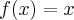 e o irracional vamos considerar o inverso dele, pela função
e o irracional vamos considerar o inverso dele, pela função 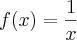 . Seguindo a ordem...
. Seguindo a ordem...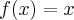
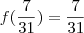
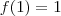
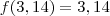
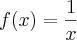
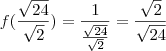



Padoan escreveu:ah sim, eu estava contando o 3,14 como irracional... falta de atenção aqui.
Obrigado!
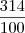 . Mas se tivesse 3,14... eu consideraria irracional, talvez por que o enunciado quer sugerir o
. Mas se tivesse 3,14... eu consideraria irracional, talvez por que o enunciado quer sugerir o  .
.

Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)