 por Larissa28 » Dom Abr 05, 2015 10:03
por Larissa28 » Dom Abr 05, 2015 10:03
Calcule os ângulos entre os planos diagonais (planos determinados pelas arestas opostas) do paralelogramo em que quatro vértices consecutivos são O(0,0,0), A(1,0,0), B(1,1,0) e C(0,1,1).
-
Larissa28
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Sáb Mar 21, 2015 17:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. de Produção
- Andamento: cursando
 por adauto martins » Seg Abr 06, 2015 12:34
por adauto martins » Seg Abr 06, 2015 12:34
vamos tomar os planos diagonais do paralelogramo...
seja o plano determinado pelos pontos,OB, cujo vetor normal eh:
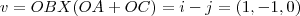
![seja o plano determ.por AC, cujo vetor normal eh:
[tex]w=OBX(OC-OA)=i-j+2k=(1,-1,2) seja o plano determ.por AC, cujo vetor normal eh:
[tex]w=OBX(OC-OA)=i-j+2k=(1,-1,2)](/latexrender/pictures/a1d2c926a7ceed7103f4e906b61c2b62.png)
...entao:
![v.w=\left|v \right|\left|w \right|cos(v,w)\Rightarrow cos(v,w)=v.w/(\left|v \right|.\left|w \right|)=(1,-1,0)(1,-1,2)/(2\sqrt[]{2})=1+1+0/2\sqrt[]{2}=1/\sqrt[]{2}=\sqrt[]{2}/2\Rightarrow (v,w)=arcos(\sqrt[]{2}/2)=\pi/4\Rightarrow (v,w)=45° v.w=\left|v \right|\left|w \right|cos(v,w)\Rightarrow cos(v,w)=v.w/(\left|v \right|.\left|w \right|)=(1,-1,0)(1,-1,2)/(2\sqrt[]{2})=1+1+0/2\sqrt[]{2}=1/\sqrt[]{2}=\sqrt[]{2}/2\Rightarrow (v,w)=arcos(\sqrt[]{2}/2)=\pi/4\Rightarrow (v,w)=45°](/latexrender/pictures/cdb2dc20405deb088f6caa6a079e8315.png)
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Qui Abr 09, 2015 16:32
por adauto martins » Qui Abr 09, 2015 16:32
oiii garota,essa minha soluçao nao esta correta,pois AC nao eh diagonal do paralelogramo solido...vou procurar resolve-lo e posto aqui,tbao...me desculpe...apareçaaaa...bons estudos
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Sex Abr 10, 2015 11:29
por adauto martins » Sex Abr 10, 2015 11:29
pelos dados do problema,temos q.
os ptos 0,A,B,C sao vertices de um pararalepido,mas o pto O,nao pertence a fase definida pelos ptos A,B,C...
pelo proprio enunciado podemops ter:D(0,0,1)eixo-z,E(0,1,0)eixo-y do pararalelpipedo,e esses ptos com os ptos dados sao suficientes p/resoluçao...
no primeiro octante temos:
ABCD definem uma face,OABE definem a fase no plano xy,logo...
os vetores OB,OC definem um plano diagonal,e AE,AC definem a outro plano diagonal...
logo,
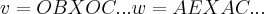
sao os vetores normais a esses planos diagonais...entao...
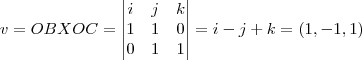
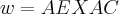
=
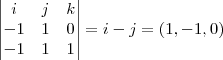
,entao...
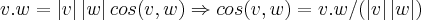
![cos(v,w)=1.1+(-1).(-1)+1.0/(\sqrt[]{3}.\sqrt[]{2})= cos(v,w)=1.1+(-1).(-1)+1.0/(\sqrt[]{3}.\sqrt[]{2})=](/latexrender/pictures/68a2bc55b7507d5a3f69352809cd0c13.png)
![\Rightarrow (v,w)=arcos(2/\sqrt[]{6}) \Rightarrow (v,w)=arcos(2/\sqrt[]{6})](/latexrender/pictures/52795b8c43a3c54360ce1e469d5a9834.png)
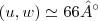
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Angulos entre planos e retas] Piramide Regular
por LucasSG » Seg Jul 08, 2013 11:36
- 1 Respostas
- 1284 Exibições
- Última mensagem por young_jedi

Seg Jul 08, 2013 20:37
Geometria Analítica
-
- PLANOS - PARALELISMO ENTRE PLANOS
por ubelima » Ter Jun 19, 2012 19:22
- 2 Respostas
- 5832 Exibições
- Última mensagem por ubelima

Qua Jun 20, 2012 01:01
Geometria Analítica
-
- Perpendicularidade entre planos
por Danilo » Seg Out 22, 2012 00:20
- 7 Respostas
- 3566 Exibições
- Última mensagem por MarceloFantini

Seg Out 29, 2012 18:03
Geometria Analítica
-
- [Interseção entre planos]
por sulafuly » Dom Mar 02, 2014 01:14
- 0 Respostas
- 2016 Exibições
- Última mensagem por sulafuly

Dom Mar 02, 2014 01:14
Geometria Analítica
-
- Interseção entre planos
por marinasaboia » Sex Jan 08, 2016 14:44
- 1 Respostas
- 3231 Exibições
- Última mensagem por RuuKaasu

Sex Jan 15, 2016 21:52
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



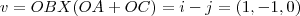
![seja o plano determ.por AC, cujo vetor normal eh:
[tex]w=OBX(OC-OA)=i-j+2k=(1,-1,2) seja o plano determ.por AC, cujo vetor normal eh:
[tex]w=OBX(OC-OA)=i-j+2k=(1,-1,2)](/latexrender/pictures/a1d2c926a7ceed7103f4e906b61c2b62.png) ...entao:
...entao:![v.w=\left|v \right|\left|w \right|cos(v,w)\Rightarrow cos(v,w)=v.w/(\left|v \right|.\left|w \right|)=(1,-1,0)(1,-1,2)/(2\sqrt[]{2})=1+1+0/2\sqrt[]{2}=1/\sqrt[]{2}=\sqrt[]{2}/2\Rightarrow (v,w)=arcos(\sqrt[]{2}/2)=\pi/4\Rightarrow (v,w)=45° v.w=\left|v \right|\left|w \right|cos(v,w)\Rightarrow cos(v,w)=v.w/(\left|v \right|.\left|w \right|)=(1,-1,0)(1,-1,2)/(2\sqrt[]{2})=1+1+0/2\sqrt[]{2}=1/\sqrt[]{2}=\sqrt[]{2}/2\Rightarrow (v,w)=arcos(\sqrt[]{2}/2)=\pi/4\Rightarrow (v,w)=45°](/latexrender/pictures/cdb2dc20405deb088f6caa6a079e8315.png)


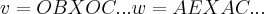 sao os vetores normais a esses planos diagonais...entao...
sao os vetores normais a esses planos diagonais...entao...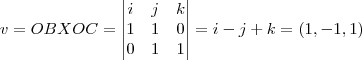
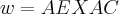 =
=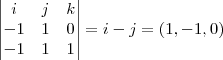 ,entao...
,entao...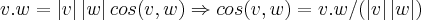
![cos(v,w)=1.1+(-1).(-1)+1.0/(\sqrt[]{3}.\sqrt[]{2})= cos(v,w)=1.1+(-1).(-1)+1.0/(\sqrt[]{3}.\sqrt[]{2})=](/latexrender/pictures/68a2bc55b7507d5a3f69352809cd0c13.png)
![\Rightarrow (v,w)=arcos(2/\sqrt[]{6}) \Rightarrow (v,w)=arcos(2/\sqrt[]{6})](/latexrender/pictures/52795b8c43a3c54360ce1e469d5a9834.png)
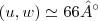



 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.