 por Danilo » Sex Mar 20, 2015 00:35
por Danilo » Sex Mar 20, 2015 00:35
Estou em dúvida no seguinte exercício. Segue o enunciado seguido de comentários/dúvidas.
Calcule
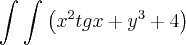
dA, onde D (eu não consegui colocar D debaixo da integral) = {(x,y)/x²+y²

2}. ok.
Vi que a região D é uma circunferência de raio
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
. Observando esse fato e colocando y em função de x eu tenho a seguinte integral:
![\int_{-\sqrt[]{2}}^{\sqrt[]{2}} \int_{-\sqrt[]{2-{x}^{2}}}^{\sqrt[]{2-{x}^{2}}}{x}^{2}tgx+{y}^{3}+4 dydx \int_{-\sqrt[]{2}}^{\sqrt[]{2}} \int_{-\sqrt[]{2-{x}^{2}}}^{\sqrt[]{2-{x}^{2}}}{x}^{2}tgx+{y}^{3}+4 dydx](/latexrender/pictures/fa80ab01d116cbf8e4265340c88c5205.png)
primeira dúvida: a integral que montei acima está correta?
Se está correta, fazendo o desenvolvimento, eu cheguei a:
![\int_{-\sqrt[]{2}}^{\sqrt[]{2}}2\sqrt[]{2-{x}^{2}}{x}^{2}tgx+8\sqrt[]{2-{x}^{2}}dx \int_{-\sqrt[]{2}}^{\sqrt[]{2}}2\sqrt[]{2-{x}^{2}}{x}^{2}tgx+8\sqrt[]{2-{x}^{2}}dx](/latexrender/pictures/e5df9897b02b096f7b65a7945c1c96b8.png)
E a partir do último ponto eu não consigo mais terminar. Não sei como fazer integração por partes com um produto com 3 fatores... Eu ficaria imensamente grato se alguém puder me ajudar!
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral dupla
por DanielFerreira » Sex Mar 16, 2012 23:56
- 2 Respostas
- 2866 Exibições
- Última mensagem por DanielFerreira

Sáb Mar 17, 2012 19:11
Cálculo: Limites, Derivadas e Integrais
-
- Integral dupla - 2
por DanielFerreira » Dom Mar 18, 2012 12:44
- 5 Respostas
- 4142 Exibições
- Última mensagem por DanielFerreira

Sex Mar 23, 2012 22:34
Cálculo: Limites, Derivadas e Integrais
-
- Integral dupla - 4
 por DanielFerreira » Sex Abr 06, 2012 19:49
por DanielFerreira » Sex Abr 06, 2012 19:49
- 4 Respostas
- 3124 Exibições
- Última mensagem por DanielFerreira

Sex Abr 06, 2012 21:05
Cálculo: Limites, Derivadas e Integrais
-
- Integral dupla - 5
por DanielFerreira » Sex Abr 06, 2012 20:00
- 2 Respostas
- 1910 Exibições
- Última mensagem por DanielFerreira

Sex Abr 06, 2012 20:16
Cálculo: Limites, Derivadas e Integrais
-
- Integral dupla - 6
 por DanielFerreira » Sáb Abr 14, 2012 22:54
por DanielFerreira » Sáb Abr 14, 2012 22:54
- 1 Respostas
- 1623 Exibições
- Última mensagem por LuizAquino

Dom Abr 15, 2012 23:45
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
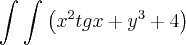 dA, onde D (eu não consegui colocar D debaixo da integral) = {(x,y)/x²+y²
dA, onde D (eu não consegui colocar D debaixo da integral) = {(x,y)/x²+y² 2}. ok.
2}. ok. ![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) . Observando esse fato e colocando y em função de x eu tenho a seguinte integral:
. Observando esse fato e colocando y em função de x eu tenho a seguinte integral: ![\int_{-\sqrt[]{2}}^{\sqrt[]{2}} \int_{-\sqrt[]{2-{x}^{2}}}^{\sqrt[]{2-{x}^{2}}}{x}^{2}tgx+{y}^{3}+4 dydx \int_{-\sqrt[]{2}}^{\sqrt[]{2}} \int_{-\sqrt[]{2-{x}^{2}}}^{\sqrt[]{2-{x}^{2}}}{x}^{2}tgx+{y}^{3}+4 dydx](/latexrender/pictures/fa80ab01d116cbf8e4265340c88c5205.png)
![\int_{-\sqrt[]{2}}^{\sqrt[]{2}}2\sqrt[]{2-{x}^{2}}{x}^{2}tgx+8\sqrt[]{2-{x}^{2}}dx \int_{-\sqrt[]{2}}^{\sqrt[]{2}}2\sqrt[]{2-{x}^{2}}{x}^{2}tgx+8\sqrt[]{2-{x}^{2}}dx](/latexrender/pictures/e5df9897b02b096f7b65a7945c1c96b8.png)

