O enunciado é simples: Resolva a Equação Diferencial
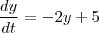
Acontece que fazendo por dois caminhos bem pouco diferentes, obtenho resultados diferentes por um sinal.
Método 1
Fazendo uma substituição:
Utilizando a propriedade do ln onde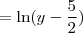
Método 2 resumido
Agora o invés de multiplicar a equação por, multiplico por
. Assim eu retiro o sinal negativo do
Mas como agora temos o "-2" e não "2" do lado direito da equação, desenvolvendo assim como no primeiro caminho iremos chegar em:
E o fato de o denominador mudar depara
não influencia porque com o jogo de sinais que é feito no primeiro método utilizando a propriedade do ln, essa diferença desaparece.
A diferença na solução é só que em uma aparece o fator
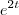 e na outra, o fator
e na outra, o fator 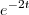
A resposta no gabarito é
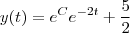 .
.Eu poderia simplesmente continuar os exercícios e sempre que aparecer uma questão assim eu multiplicar a equação por um fator que tire o sinal negativo do
 , até porque é assim que é ensinado nas resoluções do livro. Mas eu não iria conseguir dormir tranquilo haha.
, até porque é assim que é ensinado nas resoluções do livro. Mas eu não iria conseguir dormir tranquilo haha. Alguém mais experiente poderia explicar qual foi o erro que cometi para chegar em duas respostas diferentes? Sinto que deve ser algo muito simples, talvez até algum erro de sinal no meio do caminho.
Obs: Vão me desculpando se ficou confuso de entender. Tentei organizar ao máximo.

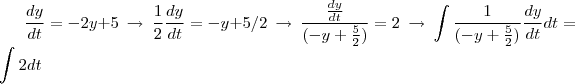
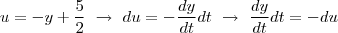
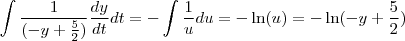
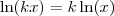
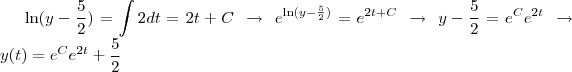
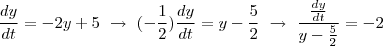

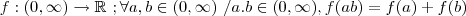
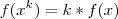 . Mas
. Mas 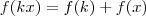 desde que
desde que  ,
, e
e 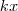 pertençam ao domínio de
pertençam ao domínio de  , que é
, que é 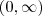 .
.
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)